
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调区间;
的单调区间;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)证明:![]() .
.
【答案】(1)分类讨论,详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)对函数![]() 求导,再根据
求导,再根据![]() 的正负分类讨论单调性即可;
的正负分类讨论单调性即可;
(2)解法一:若![]() 恒成立,即
恒成立,即![]() ,根据(1)中
,根据(1)中![]() 的单调性求出其最大值即可列式求解;解法二:若
的单调性求出其最大值即可列式求解;解法二:若![]() 恒成立,即
恒成立,即![]() 恒成立,构造函数
恒成立,构造函数![]() ,利用导数求出其最大值即可得出结论;
,利用导数求出其最大值即可得出结论;
(3)由(2)知当![]() 时,有
时,有![]() 在
在![]() 恒成立,令
恒成立,令![]() ,即可推出
,即可推出![]() ,再对不等式两边累加求和,即可推出结论.
,再对不等式两边累加求和,即可推出结论.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上是增函数;
上是增函数;
②当![]() 时,由
时,由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
则![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(2)解法一:
由(1)知![]() 时,
时,![]() 在
在![]() 递增,而
递增,而![]() ,
,
所以![]() 不恒成立,故
不恒成立,故![]() ,
,
又由(1)知![]() 时
时![]() ,
,
因为![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
解法二:
由题意知![]() ,因为
,因为![]() 恒成立,所以
恒成立,所以![]() 恒成立,
恒成立,
令![]() ,则
,则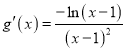 ,
,
令![]() ,令
,令![]() ,
,
所以![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,
所以![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() .
.
(3)由(2)知,当![]() 时,有
时,有![]() 在
在![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
即![]() ,从而
,从而![]() ,
,
所以![]() ,
,
即![]() .
.


科目:高中数学 来源: 题型:
【题目】将2、3、4、6、8、9、12、15共八个数排成一行,使得任意相邻两个数的最大公约数均大于1.则所有可能的排法共有()种
A. 720 B. 1014 C. 576 D. 1296
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知直线![]() 与圆O:
与圆O:![]() 相切.
相切.
(1)直线l过点(2,1)且截圆O所得的弦长为![]() ,求直线l的方程;
,求直线l的方程;
(2)已知直线y=3与圆O交于A,B两点,P是圆上异于A,B的任意一点,且直线AP,BP与y轴相交于M,N点.判断点M、N的纵坐标之积是否为定值?若是,求出该定值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B,C是一条直线道路上的三点,![]() .从A,B,C三点分别遥望电视塔M,在点A见塔在东北方向,在点B见塔在正东方向,在点C见塔在南偏东
.从A,B,C三点分别遥望电视塔M,在点A见塔在东北方向,在点B见塔在正东方向,在点C见塔在南偏东![]() ,求塔与这条道路的最短距离(精确到0.1km).
,求塔与这条道路的最短距离(精确到0.1km).
查看答案和解析>>
科目:高中数学 来源: 题型:
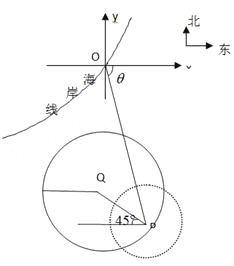
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南![]() 方向300km的海面P处,并以20km/h的速度向西偏北
方向300km的海面P处,并以20km/h的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
方向移动,台风侵袭的范围为圆形区域,当前半径为60km,并以10km/h的速度不断增大,问几小时后该城市开始受到台风的侵袭?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱柱![]() 中,侧棱
中,侧棱![]() 垂直底面,∠ACB=90°,
垂直底面,∠ACB=90°,![]() ,D为
,D为![]() 的中点,点P为AB的中点.
的中点,点P为AB的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求三棱锥B-CDP的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com