
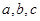 分别为角
分别为角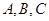 所对的三边,已知
所对的三边,已知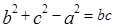
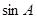 的值
的值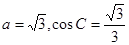 ,求边
,求边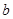 的长.
的长.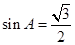 ;(Ⅱ)
;(Ⅱ)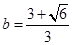 .
.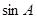 的值,可考虑利用正弦定理,也可利用面积公式
的值,可考虑利用正弦定理,也可利用面积公式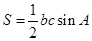 ,但本题已知
,但本题已知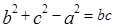 ,显然是余弦定理形式,可考虑利用余弦定理求出
,显然是余弦定理形式,可考虑利用余弦定理求出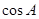 ,因此对
,因此对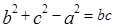 变形为
变形为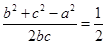 ,可得
,可得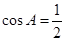 ,从而求出
,从而求出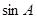 的值;(Ⅱ)若
的值;(Ⅱ)若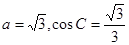 ,求边
,求边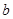 的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知
的长,可利用余弦定理,也可利用正弦定理来求,本题由(Ⅰ)知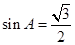 ,只要能求出
,只要能求出 ,利用余弦定理即可解决,由已知
,利用余弦定理即可解决,由已知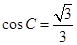 ,利用
,利用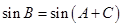 ,根据两角和与差的正弦公式即可求出,从而求出边
,根据两角和与差的正弦公式即可求出,从而求出边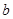 的长.
的长.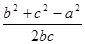 =
=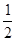 (3分)
(3分)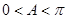 ∴sinA=
∴sinA=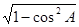 =
=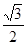 (5分)
(5分)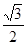 ,a=
,a=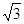 ,cosC=
,cosC=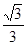
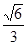 (6分)
(6分)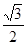 ×
×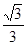 +
+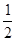 ×
×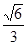 =
=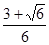 (9分)
(9分)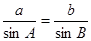
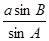 =
=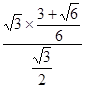 =
=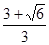 . (12分)
. (12分)

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源:不详 题型:单选题

| A.2 | B.3 | C.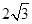 | D.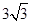 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com