Question

5．（1）如图1，矩形ABCD中AB=1，AD＞1且AD长不定，将△BCE沿CE折起，使得折起后点B落到AD边上，设∠BCE=θ，CE=L，求L关于θ的函数关系式并求L的最小值．
（2）如图2，矩形ABCD中AB=1．将矩形折起，使得点B与点F重合，当点F取遍CD边上每一个点时，得到的每一条折痕都与边AD、CB相交，求边AD长的取值范围．

Answer 1

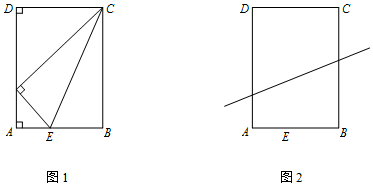
分析 （1）由图1及对称性知，CF=CB=Lcosθ，FE=BE=Lsinθ，又∠FEA=∠FCB=2θ，
得AE=FEcos2θ=Lsinθcos2θ，由AE+BE=Lsinθcos2θ+Lsinθ=1得，
L=$\frac{1}{sinθ+sinθcos2θ}$，利用导数求解
（2）当着痕GH经过AD，BC中点时，B与C重合，当矩形ABCD为正方形时，点B与A重合时，折痕刚好为对角线，AD≥BC

解答 解：（1）由图1及对称性知，
CF=CB=Lcosθ，FE=BE=Lsinθ，
又∠FEA=∠FCB=2θ，
∴AE=FEcos2θ=Lsinθcos2θ，
由AE+BE=Lsinθcos2θ+Lsinθ=1得，
L=$\frac{1}{sinθ+sinθcos2θ}$，
即L关于θ的函数关系式
L=$\frac{1}{sinθ+sinθcos2θ}$，
θ∈（0，$\frac{π}{2}$），
L′=$\frac{2cosθ（2si{n}^{2}θ-co{s}^{2}θ）}{4si{n}^{2}θco{s}^{4}θ}$=0，
可得tanθ=$\frac{\sqrt{2}}{2}$，
即有arctan$\frac{\sqrt{2}}{2}$＜θ＜$\frac{π}{2}$，L′＞0，函数L递增；
0＜θ＜arctan$\frac{\sqrt{2}}{2}$，L′＜0，函数L递减．
可得L=$\frac{1}{\frac{\sqrt{3}}{3}+\frac{\sqrt{3}}{3}×（1-2×\frac{1}{3}）}$=$\frac{3\sqrt{3}}{4}$，
此时L取得最小值为$\frac{3\sqrt{3}}{4}$；
（2）如下图，当着痕GH经过AD，BC中点时，B与C重合，
当矩形ABCD为正方形时，点B与A重合时，折痕刚好为对角线，
AD≥BC，∴AD的范围是[1，+∞）

点评 本题考查了矩形的对折问题、直角三角形的边角关系、倍角公式、三角函数的单调性、利用导数研究函数的单调性极值与最值，考查了推理能力与计算能力，属于难题．