
分析 根据一元二次方程以及一元二次不等式恒成立的问题进行转化先求出p的取值范围,然后求函数的导数,利用函数极值和导数之间的关系求出q的取值范围,结合复合命题真假关系进行求解即可.
解答 解:(1)由题设x1和x2是方程x2-ax-2=0的两个实根,得x1+x2=a且x1x2=-2,
所以|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{a}^{2}+8}$,
当a∈[-1,1]时,a2+8的最大值为9,即|x1-x2|≤3.
由题意,不等式|m2-5m-3|≥|x1-x2|
对任意的实数a∈[-1,1]恒成立的m的解集等于不等式|m2-5m-3|≥3的解集,
由此不等式得m2-5m-3≤-3①或m2-5m-3≥3②
不等式①的解集为0≤m≤5.
不等式②的解集为m≤-1或m≥6.
因此,当m≤-1或0≤m≤5或m≥6时,p是正确的…(5分)
(2)对函数f(x)=x3+mx2+(m+$\frac{4}{3}$)x+6,求导得f′(x)=3x2+2mx+m+$\frac{4}{3}$.
令f′(x)=0,即3x2+2mx+m+$\frac{4}{3}$=0.
此一元二次方程的判别式
△=4m2-12(m+$\frac{4}{3}$)=4m2-12m-16.
若△=0,则f′(x)=0有两个相等的实根,且f′(x)的符号如下:
| x | (-∞,x0) | x0 | (x0,+∞) |
| f′(x) | + | 0 | + |
| x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
点评 本题主要考查不等式恒成立以及函数极值和导数的关系,考查复合命题真假关系的应用,根据条件求出命题p,q的等价条件是解决本题的关键.综合性较强,涉及的内容较多.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
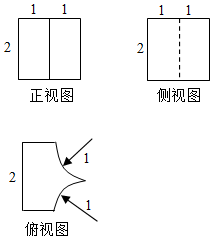 一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图曲线部分是两个半径为1的圆弧,则这个几何体的体积是( )| A. | 8-$\frac{π}{4}$ | B. | 8-$\frac{π}{2}$ | C. | 8-π | D. | 8-2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | p∨(¬q) | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
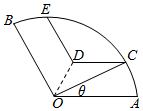 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知长方形ABCD中,AB=1,AD=$\sqrt{2}$,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
已知长方形ABCD中,AB=1,AD=$\sqrt{2}$,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com