
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线
轴的正半轴为极轴,建立极坐标系,且两种坐标系中采取相同的单位长度.曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线的参数方程是
,直线的参数方程是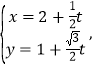 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与直线
的直角坐标方程与直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,使用手机上网成为了人们日常生活的一部分,很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求,准备推出一款流量包.该通信公司选了5个城市(总人数、经济发展情况、消费能力等方面比较接近)采用不同的定价方案作为试点,经过一个月的统计,发现该流量包的定价![]() :(单位:元/月)和购买人数
:(单位:元/月)和购买人数![]() (单位:万人)的关系如表:
(单位:万人)的关系如表:
![]()
(1)根据表中的数据,运用相关系数进行分析说明,是否可以用线性回归模型拟合![]() 与
与![]() 的关系?并指出是正相关还是负相关;
的关系?并指出是正相关还是负相关;
(2)①求出![]() 关于
关于![]() 的回归方程;
的回归方程;
②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月,请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.
参考数据:![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数 ,回归直线方程
,回归直线方程![]() ,
,
其中 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的选项是( )
A. 若![]() 为真命题,则
为真命题,则![]() 为真命题 B.
为真命题 B. ![]() ,使得
,使得![]() C. “平面向量
C. “平面向量![]() 与
与![]() 的夹角为钝角”的充分不必要条件是“
的夹角为钝角”的充分不必要条件是“![]() ” D. 在锐角
” D. 在锐角![]() 中,必有
中,必有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过圆![]() :
:![]() 上一动点
上一动点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() .
.
(Ⅰ)求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() ,
,![]() 两点,过
两点,过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 交圆
交圆![]() 于
于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图4,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,过
,过![]() 作平面分别交线段
作平面分别交线段![]() 于点
于点![]() .
.

(1)证明:![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的线面角的正切值为
所成的线面角的正切值为![]() ,则当点
,则当点![]() 在线段
在线段![]() 的何处时,直线
的何处时,直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017-2018学年安徽省六安市第一中学高三上学期第二次月考)已知函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求
没有交点,求![]() 的取值范围;
的取值范围;
(3)若函数![]() ,是否存在实数
,是否存在实数![]() 使得
使得![]() 的最小值为0,若存在,求出
的最小值为0,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com