
【题目】若曲线![]() 和
和![]() 上分别存在点
上分别存在点![]() ,使得
,使得![]() 是以原点
是以原点![]() 为直角顶点的直角三角形,AB交y轴于C,且
为直角顶点的直角三角形,AB交y轴于C,且![]() 则实数
则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
由题意设出A,B的坐标,代入函数解析式,利用![]() 把B的坐标用A的坐标表示,由
把B的坐标用A的坐标表示,由![]() 可得关于A的横坐标的方程,分离参数a后构造函数h(x)
可得关于A的横坐标的方程,分离参数a后构造函数h(x)![]() ,利用导数求其在(e﹣1<x<e2﹣1)上的单调性,得到函数的值域得答案.
,利用导数求其在(e﹣1<x<e2﹣1)上的单调性,得到函数的值域得答案.
设A(x1,y1),y1=f(x1)![]() ,B(x2,y2),y2=g(x2)=﹣x23+x22(x<0),又
,B(x2,y2),y2=g(x2)=﹣x23+x22(x<0),又![]() ,
,
则![]() ,x2=﹣2x1,∴
,x2=﹣2x1,∴![]() .
.
![]() ,
,![]() ,
,
由题意,![]() ,即
,即![]() 0,
0,
∴![]() ,
,
∵e﹣1<x1<e2﹣1,
∴![]() ,
,
则![]() .
.
设h(x)![]() ,则h′(x)
,则h′(x)![]() ,令
,令![]() ,则u′(x)=
,则u′(x)=![]() =
=![]() >0在e﹣1<x<e2﹣1恒成立,所以
>0在e﹣1<x<e2﹣1恒成立,所以![]() 单增,所以
单增,所以![]() >
>![]() =
=![]() >0,∴h′(x)>0,
>0,∴h′(x)>0,
即函数h(x)![]() 在(e﹣1<x<e2﹣1)上为增函数,
在(e﹣1<x<e2﹣1)上为增函数,
则![]() ,
,
即4e-2<a![]() .
.
∴实数a的取值范围是![]() .
.
故选:B.


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,求实数
,求实数![]() ,
,![]() 的值;
的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处取得极值,求实数
两处取得极值,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )和圆
)和圆![]() :
:![]() ,
,![]() 分别是椭圆的左、右两焦点,过
分别是椭圆的左、右两焦点,过![]() 且倾斜角为
且倾斜角为![]() (
(![]() )的动直线
)的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点(如图所示,点
两点(如图所示,点![]() 在
在![]() 轴上方).当
轴上方).当![]() 时,弦
时,弦![]() 的长为
的长为![]() .
.

(1)求圆![]() 与椭圆
与椭圆![]() 的方程;
的方程;
(2)若![]() 依次成等差数列,求直线
依次成等差数列,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“吃鸡”游戏中,某玩家被随机降落在边长为4的正三角形绝地岛上,已知在离三个顶点距离都大于![]() 的区域内可以搜集枪支弹药、防弹衣、医疗包等生存物资,则该玩家能够获得生存物资的概率为( )
的区域内可以搜集枪支弹药、防弹衣、医疗包等生存物资,则该玩家能够获得生存物资的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,且函数
,且函数![]() 在
在![]() 处取得最大值.
处取得最大值.
(1)求![]() 的最小值,并求出此时函数
的最小值,并求出此时函数![]() 的解析式和最小正周期;
的解析式和最小正周期;
(2)在(1)的条件下,先将![]() 的图像上的所有点向右平移
的图像上的所有点向右平移![]() 个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),然后将所得图像上所有的点向下平移
个单位,再把所得图像上所有点的横坐标伸长为原来的2倍(纵坐标不变),然后将所得图像上所有的点向下平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像.若在区间
的图像.若在区间![]() 上,方程
上,方程![]() 有两个不相等的实数根,求实数a的取值范围;
有两个不相等的实数根,求实数a的取值范围;
(3)在(1)的条件下,已知点P是函数![]() 图像上的任意一点,点Q为函数
图像上的任意一点,点Q为函数![]() 图像上的一点,点
图像上的一点,点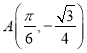 ,且满足
,且满足![]() ,求
,求![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将边长为2的正方形ABCD沿PD、PC翻折至A、B两点重合,其中P是AB中点,在折成的三棱锥A(B)-PDC中,点Q在平面PDC内运动,且直线AQ与棱AP所成角为60,则点Q运动的轨迹是
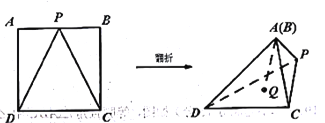
A. 圆 B. 椭圆 C. 双曲线 D. 抛物线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com