
【题目】已知实数x、y满足  ,目标函数z=x+ay.
,目标函数z=x+ay.
(1)当a=﹣2时,求目标函数z的取值范围;
(2)若使目标函数取得最小值的最优解有无数个,求 ![]() 的最大值.
的最大值.
【答案】
(1)解:当a=﹣2时,z=x﹣2y,由z=x﹣2y得y= ![]() ,
,
作出不等式组对应的平面区域如图(阴影部分ABC):
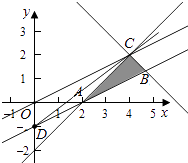
平移直线y= ![]() ,
,
由图象可知当直线y= ![]() ,过点C时,直线y=
,过点C时,直线y= ![]() 的截距最大,此时z最小,
的截距最大,此时z最小,
由 ![]() ,解得
,解得 ![]() ,即C(4,2).此时z=4﹣2×2=4﹣4=0,
,即C(4,2).此时z=4﹣2×2=4﹣4=0,
当直线与x﹣2y﹣2=0重合时,直线y= ![]() 的截距最小,此时z最大,
的截距最小,此时z最大,
此时z=2,即0≤z≤2
(2)解:若a>0,由题意知最优解应该在线段BC上取得,但此时取到的最大值不满足条件.
当a=0,不满足条件.
若a<0,最优解应该在线段AC上取得,故直线x+ay=0与AC平行,
则kAC=1=﹣ ![]() ,得a=﹣1.
,得a=﹣1.
![]() =
= ![]() 的几何意义是区域内的点到点D(﹣1,0)的斜率,
的几何意义是区域内的点到点D(﹣1,0)的斜率,
由图象知当点与C(4,2)重合时, ![]() 取得最大值
取得最大值 ![]() .
.
【解析】(1)当a=﹣2时,z=x﹣2y,由z=x﹣2y得y= ![]() ,平移直线进行求解即可.(2)根据目标函数取得最小值的最优解有无数个,求出a=﹣1,利用直线斜率的几何意义进行求解即可.
,平移直线进行求解即可.(2)根据目标函数取得最小值的最优解有无数个,求出a=﹣1,利用直线斜率的几何意义进行求解即可.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=92n﹣1 , n∈N* . (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=(n﹣1)an , 数列{bn}的前n项和为Sn , 若不等式Sn>kan+16n﹣26对一切n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲抛掷均匀硬币2017次,乙抛掷均匀硬币2016次,下列四个随机事件的概率是0.5的是( )
①甲抛出正面次数比乙抛出正面次数多;
②甲抛出反面次数比乙抛出正面次数少;
③甲抛出反面次数比甲抛出正面次数多;
④乙抛出正面次数与乙抛出反面次数一样多.
A.①②
B.①③
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A.在等差数列{an}中,若ap+aq=ar+aδ , 则p+q=r+δ
B.已知数列{an}的前n项和为Sn , 若{an}是等比数列,则Sk , S2k﹣Sk , S3k﹣S2k也是等比数列
C.在数列{an}中,若ap+aq=2ar , 则ap , ar , aq成等差数列
D.在数列{an}中,若ap?aq=a ![]() ,则ap , ar , aq成等比数列
,则ap , ar , aq成等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R.当x<0时,f(x)=x3﹣1;当﹣1≤x≤1时,f(﹣x)=﹣f(x);当x> ![]() 时,f(x+
时,f(x+ ![]() )=f(x﹣
)=f(x﹣ ![]() ).则f(6)=( )
).则f(6)=( )
A.﹣2
B.﹣1
C.0
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名运动员进行射击训练,已知他们击中目标的环数均稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如表:
甲运动员
射击环数 | 频数 | 频率 |
7 | 10 | |
8 | 10 | |
9 | x | |
10 | 30 | y |
合计 | 100 | 1 |
乙运动员
射击环数 | 频数 | 频率 |
7 | 6 | |
8 | 10 | |
9 | z | 0.4 |
10 | ||
合计 | 80 |
如果将频率视为概率,回答下面的问题:
(1)写出x,y,z的值;
(2)求甲运动员在三次射击中,至少有一次命中9环(含9环)以上的概率;
(3)若甲运动员射击2次,乙运动员射击1次,用ξ表示这三次中射击击中9环的次数,求ξ的概率分布列及Eξ.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com