
【题目】已知函数f(x)=![]() 在点(1,1)处的切线方程为x+y=2.
在点(1,1)处的切线方程为x+y=2.
(1)求a,b的值;
(2)对函数f(x)定义域内的任一个实数x,不等式f(x)-![]() <0恒成立,求实数m的取值范围.
<0恒成立,求实数m的取值范围.
【答案】(1)![]() (2)m的取值范围是(1,+∞).
(2)m的取值范围是(1,+∞).
【解析】试题分析:(1)先根据导数几何意义得f′(1)=-1,再根据![]() 解得a,b的值;(2)先变量分离得
解得a,b的值;(2)先变量分离得![]() 最大值,再利用导数研究函数
最大值,再利用导数研究函数![]() 单调性,进而得最大值,即得实数m的取值范围.
单调性,进而得最大值,即得实数m的取值范围.
试题解析:(1)由题f′(x)=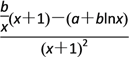 ,
,
又直线x+y=2的斜率为-1.2分
∴f′(1)=-1,即![]() =-1.3分
=-1.3分
又(1,1)点在函数f(x)=![]() 的图象上,
的图象上,
故![]() =1,
=1,
由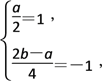 解得
解得![]()
(2)由(1)得f(x)=![]() (x>0),由f(x)<
(x>0),由f(x)<![]() 及x>0
及x>0![]() <m,8分
<m,8分
令g(x)=![]()
g′(x)=![]()
=![]() ,
,
令h(x)=1-x-ln xh′(x)=-1-![]() <0(x>0),故h(x)在区间(0,+∞)上是减函数,
<0(x>0),故h(x)在区间(0,+∞)上是减函数,
故当0<x<1时,h(x)>h(1)=0,
当x>1时,h(x)<h(1)=0.10分
从而当0<x<1时,g′(x)>0,当x>1时,
g′(x)<0g(x)在(0,1)是增函数,在(1,+∞)是减函数.11分
故g/span>(x)max=g(1)=1,要使![]() <m成立,只需m>1,
<m成立,只需m>1,
故m的取值范围是(1,+∞).


科目:高中数学 来源: 题型:
【题目】函数f(x)=![]() x3-kx,其中实数k为常数.
x3-kx,其中实数k为常数.
(1)当k=4时,求函数的单调区间;
(2)若曲线y=f(x)与直线y=k只有一个交点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右顶点与右焦点的距离为
右顶点与右焦点的距离为![]() ,短轴长为
,短轴长为![]()
(I)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为![]() 求直线AB的方程。
求直线AB的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ex-![]() (x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
(x<0)与g(x)=x2+ln(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
A. (-∞,![]() ) B. (-∞,
) B. (-∞,![]() )
)
C. (-![]() ,
, ![]() ) D. (-
) D. (-![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
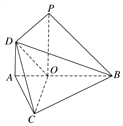
【题目】如图,在△ABC中,∠ABC=45°,点O在AB上,且OB=OC=![]() AB,PO⊥平面ABC,DA∥PO,DA=AO=
AB,PO⊥平面ABC,DA∥PO,DA=AO=![]() PO.
PO.
(1)求证:PB∥平面COD;
(2)求二面角O-CD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
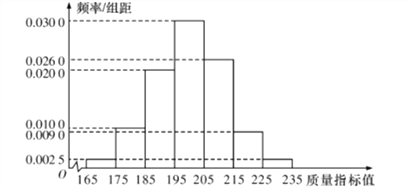
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
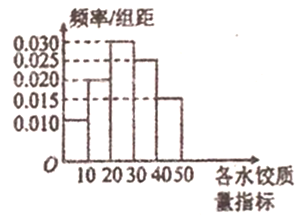
(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com