
【题目】命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;命题q:函数f(x)=lagax在(0,+∞)上递增,若p∨q为真,而p∧q为假,求实数a的取值范围.
【答案】解:命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;
①若命题p正确,则△=(2a)2﹣42<0,即﹣2<a<2;
②命题q:函数f(x)=logax在(0,+∞)上递增a>1,
∵p∨q为真,而p∧q为假,
∴p、q一真一假,
当p真q假时,有 ![]() ,
,
∴﹣2<a≤1;
当p假q真时,有 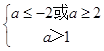 ,
,
∴a≥2
∴综上所述,﹣2<a≤1或a≥2.
即实数a的取值范围为(﹣2,1]∪[2,+∞).
【解析】依题意,可分别求得p真、q真时m的取值范围,再由p∨q为真,而p∧q为假求得实数a的取值范围即可.
【考点精析】利用复合命题的真假对题目进行判断即可得到答案,需要熟知“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真.


科目:高中数学 来源: 题型:
【题目】已知数列{an}是等比数列,a1=2,a3=18.数列{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{an},{bn}的通项公式;
(2)设Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….试比较Pn与Qn的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A,B,C是△ABC的三个内角.
(1)3cos(B﹣C)﹣1=6cosBcosC,求cosA的值;
(2)若sin(A+ ![]() )=2cosA,求A.
)=2cosA,求A.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<k<4,直线l1:kx﹣2y﹣2k+8=0和直线l:2x+k2y﹣4k2﹣4=0与两坐标轴围成一个四边形,则使得这个四边形面积最小的k值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com