
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期为π,且其图象向左平移
)的最小正周期为π,且其图象向左平移 ![]() 个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
个单位后得到函数g(x)=cosωx的图象,则函数f(x)的图象( )
A.关于直线x= ![]() 对称
对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于点( ![]() ,0)对称
,0)对称
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为 (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)设曲线C经过伸缩变换 得到曲线,设M(x,y)为
得到曲线,设M(x,y)为![]() 上任意一点,求
上任意一点,求![]() 的最小值,并求相应的点M的坐标.
的最小值,并求相应的点M的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某贫困地区有1500户居民,其中平原地区1050户,山区450户,为调查该地区2017年家庭收入情况,从而更好地实施“精准扶贫”,采用分层抽样的方法,收集了150户家庭2017年年收入的样本数据(单位:万元)
(I)应收集多少户山区家庭的样本数据?
(Ⅱ)根据这150个样本数据,得到2017年家庭收入的频率分布直方图(如图所示),其中样本数据分组区间为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
.如果将频率率视为概率,估计该地区2017年家庭收入超过1.5万元的概率;
(Ⅲ)样本数据中,由5户山区家庭的年收入超过2万元,请完成2017年家庭收入与地区的列联表,并判断是否有90%的把握认为“该地区2017年家庭年收入与地区有关”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超过2万元 | 不超过2万元 | 总计 | |
平原地区 | |||
山区 | 5 | ||
总计 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题:①函数![]() 的值域是
的值域是![]() ;
;
②为了得到函数![]() 的图象,只需把函数
的图象,只需把函数![]() 图象上的所有点向右平移
图象上的所有点向右平移![]() 个单位长度;
个单位长度;
③当![]() 或
或![]() 时,幂函数
时,幂函数![]() 的图象都是一条直线;
的图象都是一条直线;
④已知函数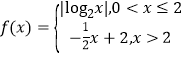 ,若
,若![]() 互不相等,且
互不相等,且![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .
.
其中正确的命题个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() .
.
(1)求![]() 的值并求函数
的值并求函数![]() 的值域;
的值域;
(2)若关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的最大值为
的最大值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个五个命题:
①“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
②对于命题![]() ,使得
,使得![]() ,则
,则![]() ,均有
,均有![]() ;
;
③命题“若![]() ,则方程
,则方程![]() 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程![]()
![]() 没有实数根,则
没有实数根,则![]() ”;
”;
④函数![]() 只有
只有![]() 个零点;
个零点;
⑤![]() 使
使![]() 是幂函数,且在
是幂函数,且在![]() 上单调递减.
上单调递减.
其中是真命题的个数为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() )
)
(1)若在区间[0,1]上有最大值1和最小值-2.求a,b的值;
(2)在(1)条件下,若在区间![]() 上,不等式f(x)
上,不等式f(x)![]()
![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com