
在直角梯形ABCD中,AB=2DC=2AD=2,∠DAB=∠ADC =90°,将△DBC沿BD向上折起,使面ABD垂直于面BDC,则C-DAB三棱锥的外接球的体积为________.
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:填空题
如图,直线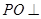 平面
平面 ,垂足为
,垂足为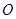 ,直线
,直线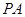 是平面
是平面 的一条斜线,斜足为
的一条斜线,斜足为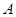 ,其中
,其中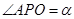 ,过点
,过点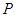 的动直线
的动直线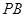 交平面
交平面 于点
于点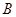 ,
,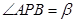 ,则下列说法正确的是___________.
,则下列说法正确的是___________.
①若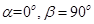 ,则动点B的轨迹是一个圆;
,则动点B的轨迹是一个圆;
②若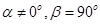 ,则动点B的轨迹是一条直线;
,则动点B的轨迹是一条直线;
③若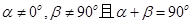 ,则动点B的轨迹是抛物线;
,则动点B的轨迹是抛物线;
④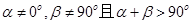 ,则动点B的轨迹是椭圆;
,则动点B的轨迹是椭圆;
⑤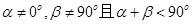 ,则动点B的轨迹是双曲线.
,则动点B的轨迹是双曲线.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若 ,
, ,则
,则 ;
;
②若 ,
, ,则
,则 ;
;
③若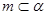 ,
,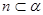 ,
, ,
, ,则
,则 ;
;
④若 ,
, ,
, ,
,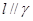 ,则
,则 。
。
其中命题正确的是 .(填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com