
【题目】设函数![]() ,其中
,其中![]() .
.
(1)若![]() ,求过点
,求过点![]() 且与曲线
且与曲线![]() 相切的直线方程;
相切的直线方程;
(2)若函数![]() 有两个零点
有两个零点![]() .
.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
【答案】(1) y=-![]() x-1 (2)①(0,e)②见解析
x-1 (2)①(0,e)②见解析
【解析】试题分析:(1) 当a=0时,f(x)=-1-lnx,f ′(x)=-![]() .设切点为T(x0,-1-lnx0),得到切线方程,由于过
.设切点为T(x0,-1-lnx0),得到切线方程,由于过![]() ,得到关于x0的方程,解之即可得到与曲线
,得到关于x0的方程,解之即可得到与曲线![]() 相切的直线方程;
相切的直线方程;
(2)①要使函数f(x)有两个零点,只需考虑函数的最值与零的关系即可;②由x1,x2是函数f(x)的两个零点(不妨设x1<x2),得 两式相减,得
两式相减,得 ![]() a(x12-x22)-ln
a(x12-x22)-ln![]() =0,即
=0,即![]() a(x1+x2) (x1-x2)-ln
a(x1+x2) (x1-x2)-ln![]() =0.f ′(x1)+f ′(x2)<0等价于ax1-
=0.f ′(x1)+f ′(x2)<0等价于ax1-![]() +ax2-
+ax2-![]() <0,即a(x1+x2)-
<0,即a(x1+x2)-![]() -
-![]() <0,把a换掉构造新函数即可.
<0,把a换掉构造新函数即可.
试题解析:
(1)当a=0时,f(x)=-1-lnx,f ′(x)=-![]() .
.
设切点为T(x0,-1-lnx0),
则切线方程为:y+1+lnx0=-![]() ( x-
( x-![]() ).
).
因为切线过点(0,-1),所以 -1+1+ln x0=-![]() (0-x0),解得x0=e.
(0-x0),解得x0=e.
所以所求切线方程为y=-![]() x-1.
x-1.
(2)① f ′(x)=ax-![]() =
=![]() ,x>0.
,x>0.
(i) 若a≤0,则f ′(x)<0,所以函数f(x)在(0,+∞)上单调递减,
从而函数f(x)在(0,+∞)上至多有1个零点,不合题意.
(ii)若a>0,由f ′(x)=0,解得x=![]() .
.
当0<x<![]() 时, f ′(x)<0,函数f(x)单调递减;当x>
时, f ′(x)<0,函数f(x)单调递减;当x>![]() 时, f ′(x)>0,f(x)单调递增,
时, f ′(x)>0,f(x)单调递增,
所以f(x)min=f(![]() )=
)=![]() -ln
-ln![]() -1=-
-1=-![]() -ln
-ln![]() .
.
要使函数f(x)有两个零点,首先 -![]() -ln
-ln![]() <0,解得0<a<e
<0,解得0<a<e
当0<a<e时, ![]() >
>![]() >
>![]() .
.
因为f(![]() )=
)=![]() >0,故f(
>0,故f(![]() )·f(
)·f(![]() )<0.
)<0.
又函数f(x)在(0, ![]() )上单调递减,且其图像在(0,
)上单调递减,且其图像在(0, ![]() )上不间断,
)上不间断,
所以函数f(x)在区间(0, ![]() )内恰有1个零点.
)内恰有1个零点.
考察函数g(x)=x-1-lnx,则g′(x)=1-![]() =
=![]() .
.
当x∈(0,1)时,g′(x)<0,函数g(x)在(0,1)上单调递减;
当x∈(1,+∞)时,g′(x)>0,函数g(x)在(1,+∞)上单调递增,
所以g(x)≥g(1)=0,故f(![]() )=
)=![]() -1-ln
-1-ln![]() ≥0.
≥0.
因为![]() -
-![]() =
=![]() >0,故
>0,故![]() >
>![]() .
.
因为f(![]() )·f(
)·f(![]() )≤0,且f(x)在(
)≤0,且f(x)在(![]() ,+∞)上单调递增,其图像在(
,+∞)上单调递增,其图像在(![]() ,+∞)上不间断,
,+∞)上不间断,
所以函数f(x)在区间(![]() ,
, ![]() ] 上恰有1个零点,即在(
] 上恰有1个零点,即在(![]() ,+∞)上恰有1个零点.
,+∞)上恰有1个零点.
综上所述,a的取值范围是(0,e).
②由x1,x2是函数f(x)的两个零点(不妨设x1<x2),得
两式相减,得 ![]() a(x12-x22)-ln
a(x12-x22)-ln![]() =0,即
=0,即![]() a(x1+x2) (x1-x2)-ln
a(x1+x2) (x1-x2)-ln![]() =0,
=0,
所以a(x1+x2)=![]() .
.
f ′(x1)+f ′(x2)<0等价于ax1-![]() +ax2-
+ax2-![]() <0,即a(x1+x2)-
<0,即a(x1+x2)-![]() -
-![]() <0,
<0,
即![]() -
-![]() -
-![]() <0,即2ln
<0,即2ln![]() +
+![]() -
-![]() >0.
>0.
设h(x)=2lnx+![]() -x,x∈(0,1).则h′(x)=
-x,x∈(0,1).则h′(x)=![]() -
-![]() -1=
-1=![]() =-
=-![]() <0,
<0,
所以函数h(x)在(0,1)单调递减,所以h(x)>h(1)=0.
因为![]() ∈(0,1),所以2ln
∈(0,1),所以2ln![]() +
+![]() -
-![]() >0,
>0,


科目:高中数学 来源: 题型:
【题目】[2018·沧州质检]对于椭圆![]() ,有如下性质:若点
,有如下性质:若点![]() 是椭圆上的点,则椭圆在该点处的切线方程为
是椭圆上的点,则椭圆在该点处的切线方程为![]() .利用此结论解答下列问题.点
.利用此结论解答下列问题.点![]() 是椭圆
是椭圆![]() 上的点,并且椭圆在点
上的点,并且椭圆在点![]() 处的切线斜率为
处的切线斜率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若动点![]() 在直线
在直线![]() 上,经过点
上,经过点![]() 的直线
的直线![]() ,
,![]() 与椭圆
与椭圆![]() 相切,切点分别为
相切,切点分别为![]() ,
,![]() .求证:直线
.求证:直线![]() 必经过一定点.
必经过一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中装有四张大小形状均相同的卡片,卡片上分别标有数![]() 其中
其中![]() 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响).
(1)求事件![]() “在一次试验中,得到的数为虚数”的概率
“在一次试验中,得到的数为虚数”的概率![]() 与事件
与事件![]() “在四次试验中,
“在四次试验中,
至少有两次得到虚数” 的概率![]() ;
;
(2)在两次试验中,记两次得到的数分别为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 为等边三角形,
为等边三角形,![]() ,且
,且![]() ,O,M分别为
,O,M分别为![]() ,
,![]() 的中点.
的中点.
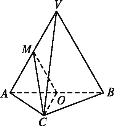
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 是线段
是线段![]() 上一点,满足平面
上一点,满足平面![]() 平面
平面![]() ,试说明点的位置
,试说明点的位置![]() ;
;
(Ⅲ)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
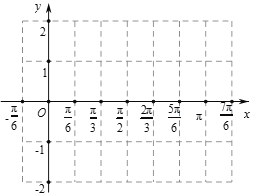
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
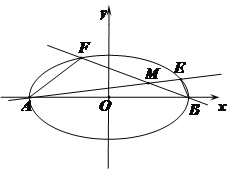
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且短轴长为2.
,且短轴长为2.
(1)求椭圆的标准方程;
(2)已知![]() 分别为椭圆的左右顶点,
分别为椭圆的左右顶点, ![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 与
与![]() 分别与椭圆交于
分别与椭圆交于![]() 两点,
两点,
(i)用![]() 表示点
表示点![]() 的纵坐标;
的纵坐标;
(ii)若![]() 面积是
面积是![]() 面积的5倍,求
面积的5倍,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com