
| PE |
| PF |
| 1 |
| 2 |
| 1 |
| 2 |
| PE |
| PF |
| PM |
| PE |
| PF |
| 4PM2-(PE2+PF2) |
| 2 |
| PE |
| PF |
| PE |
| PF |
| |0-2+1| | ||
|
| ||
| 2 |
| PE |
| PF |
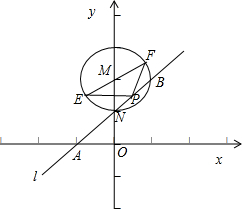 解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,
解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,| PE |
| PF |
| PM |
| PE |
| PF |
| PE |
| PF |
| PM |
| PE |
| PF |
4
| ||||||
| 2 |
| 4PM2-(PE2+PF2) |
| 2 |
| PE |
| PF |
| PE |
| PF |
| PE |
| PF |
4PM2-2
| ||||
| 2 |
| PE |
| PF |
| PE |
| PF |
| PE |
| PF |
| PE |
| PF |
| |0-2+1| | ||
|
| ||
| 2 |
| PE |
| PF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
| QM |
| QP |
| 1 |
| 2 |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M查看答案和解析>>
科目:高中数学 来源:学习周报 数学 人教课标高一版(A必修2) 2009-2010学年 第24期 总180期 人教课标高一版 题型:022
如图,已知点P是直线l:3x+4y+8=0上的动点,PA,PB是圆x2+y2-2x-2y+1=0的两条切线,A,B是切点,C是圆心,则四边形PACB面积的最小值是________.
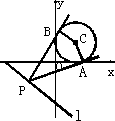
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
A.x+3y=0 B.2x-y=0 C.x+3y+2=0 D.2x-y-3=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com