
【题目】定义:如果函数y=f(x)在定义域内给定区间[a,b]上存在x0(a<x0<b),满足f(x0)= ![]() ,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
,则称函数y=f(x)是[a,b]上的“平均值函数”,x0是它的一个均值点.例如y=|x|是[﹣2,2]上的平均值函数,0就是它的均值点.若函数f(x)=x2﹣mx﹣1是[﹣1,1]上的“平均值函数”,则实数m的取值范围是 .
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
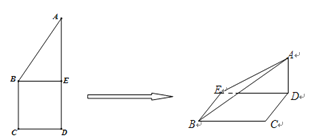
【题目】如图正方形![]() 的边长为
的边长为![]() ,已知
,已知![]() ,将
,将![]() 沿
沿![]() 边折起,折起后
边折起,折起后![]() 点在平面
点在平面![]() 上的射影为
上的射影为![]() 点,则翻折后的几何体中有如下描述:
点,则翻折后的几何体中有如下描述:
①![]() 与
与![]() 所成角的正切值是
所成角的正切值是![]() ;
;
②![]() ∥
∥![]() ;
;
③![]() 的体积是
的体积是![]() ;
;
④平面![]() ⊥平面
⊥平面![]() ;
;
⑤直线![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.
其中正确的有 .(填写你认为正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】AB是☉O的直径,点C是☉O上的动点(点C不与A,B重合),过动点C的直线VC垂直于☉O所在的平面,D,E分别是VA,VC的中点,则下列结论中正确的是________(填写正确结论的序号).
(1)直线DE∥平面ABC.
(2)直线DE⊥平面VBC.
(3)DE⊥VB.
(4)DE⊥AB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x﹣1)的对称轴为x=1,f(x+1)= ![]() (f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
(f(x)≠0),且在区间(1,2)上单调递减,已知α、β是钝角三角形中两锐角,则f(sinα)和f(cosβ)的大小关系是( )
A.f(sinα)>f(cosβ)
B.f(sinα)<f(cosβ)
C.f(sinα)=f(cosβ)
D.以上情况均有可能
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是甲、乙两人在一次射击比赛中中靶的情况(击中靶中心的圆面为10环,靶中各数字表示该数字所在圆环被击中所得的环数),每人射击了6次.
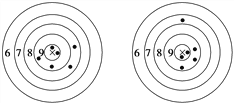
甲射击的靶 乙射击的靶
(1)请用列表法将甲、乙两人的射击成绩统计出来;
(2)请你用学过的统计知识,对甲、乙两人这次的射击情况进行比较.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(-![]() ,0),B(0,-
,0),B(0,-![]() ),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
(1)求证:A,B关于直线l对称.
(2)当1<k<![]() 时,求直线l在y轴上的截距b的取值范围.
时,求直线l在y轴上的截距b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度![]() (单位:千克/年)是养殖密度
(单位:千克/年)是养殖密度![]() (单位:尾/立方米)的函数.当
(单位:尾/立方米)的函数.当![]() 不超过
不超过![]() 尾/立方米时,
尾/立方米时, ![]() 的值为
的值为![]() 千克/年;当
千克/年;当![]() 时,
时, ![]() 是
是![]() 的一次函数,且当
的一次函数,且当![]() 时,
时, ![]() .
.
(![]() )当
)当![]() 时,求
时,求![]() 关于
关于![]() 的函数的表达式.
的函数的表达式.
(![]() )当养殖密度
)当养殖密度![]() 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数 ![]() 的单调递减区间是( )
的单调递减区间是( ) 
A.(﹣∞,﹣2)
B.(﹣∞,1)
C.(﹣2,4)
D.(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com