已知数列{an}、{bn},且通项公式分别为an=3n-2,bn=n2,现抽出数列{an}、{bn}中所有相同的项并按从小到大的顺序排列成一个新的数列{cn},则可以推断:
(1)c50= (填数字);
(2)c2k-1= (用k表示).
【答案】
分析:由a
n=3n-2,b
n=n
2,数列{a
n}、{b
n}中所有相同的项并按从小到大的顺序排列成一个新的数列{c
n},可得数列{c
n}的通项公式满足:当n为奇数时,c
n=(3•
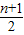
-2)
2,当n为偶数时,c
n=(3•
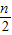
-1)
2,分别代入可得答案.
解答:解:∵a
n=3n-2,b
n=n
2,
数列{c
n}为数列{a
n}、{b
n}中所有相同的项并按从小到大的顺序排列成一个新的数列
则c
n中各项应满足:①比三的倍数多1;②是一个完全平方数
当n为奇数时,c
n=(3•
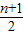
-2)
2,
当n为偶数时,c
n=(3•
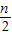
-1)
2,
(1)∵50为偶数
故c
50=(3•
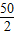
-1)
2=74
2=5476
(2)∵2k-1为奇数
∴c
2k-1=(3•
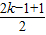
-2)
2=(3k-2)
2
故答案为:5476,(3k-2)
2点评:本题考查的知识点是数列的通项公式,本题难度较大,其中解答的关键是根据已知两个数列{a
n}、{b
n}的通项公式,求出数列{c
n}的通项公式.

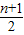 -2)2,当n为偶数时,cn=(3•
-2)2,当n为偶数时,cn=(3•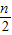 -1)2,分别代入可得答案.
-1)2,分别代入可得答案.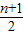 -2)2,
-2)2,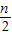 -1)2,
-1)2,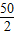 -1)2=742=5476
-1)2=742=5476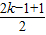 -2)2=(3k-2)2
-2)2=(3k-2)2

 同步奥数系列答案
同步奥数系列答案