
【题目】如图,点P在正方体ABCD﹣A1B1C1D1的表面上运动,且P到直线BC与直线C1D1的距离相等,如果将正方体在平面内展开,那么动点P的轨迹在展开图中的形状是( )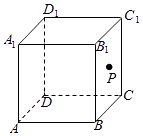
A.
B.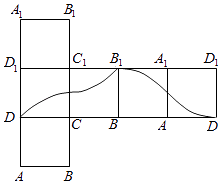
C.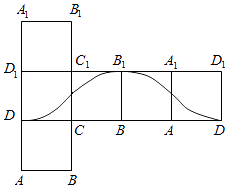
D.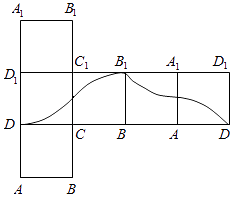
科目:高中数学 来源: 题型:
【题目】某地区拟建立一个艺术搏物馆,采取竞标的方式从多家建筑公司选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标.现从建筑设计院聘请专家设计了一个招标方案:两家公司从6个招标总是中随机抽取3个总题,已知这6个招标问题中,甲公司可正确回答其中4道题目,而乙公司能正面回答每道题目的概率均为 ![]() ,甲、乙两家公司对每题的回答都是相独立,互不影响的.
,甲、乙两家公司对每题的回答都是相独立,互不影响的.
(1)求甲、乙两家公司共答对2道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”: 2 ![]() =
= ![]() ,3
,3 ![]() =
= ![]() ,4
,4 ![]() =
= ![]() ,5
,5 ![]() =
= ![]()
则按照以上规律,若8 ![]() =
= ![]() 具有“穿墙术”,则n=( )
具有“穿墙术”,则n=( )
A.7
B.35
C.48
D.63
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复平面上点Z1 , Z2 , …,Zn , …分别对应复数z1 , z2 , …,zn , …;
(1)设z=r(cosα+isinα),(r>0,α∈R),用数学归纳法证明:zn=rn(cosnα+isinnα),n∈Z+
(2)已知 ![]() ,且
,且 ![]() (cosα+isinα)(α为实常数),求出数列{zn}的通项公式;
(cosα+isinα)(α为实常数),求出数列{zn}的通项公式;
(3)在(2)的条件下,求 ![]() |+….
|+….
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=4 ![]() ,AD=2
,AD=2 ![]() ,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.
,将△ABD沿BD折起,使得点A折起至A′,设二面角A′﹣BD﹣C的大小为θ.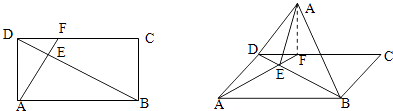
(1)当θ=90°时,求A′C的长;
(2)当cosθ= ![]() 时,求BC与平面A′BD所成角的正弦值.
时,求BC与平面A′BD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)﹣x2+(2﹣a)x﹣a(a∈R)若存在唯一的正整数x0 , 使得f(x0)>0,则实数a的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ]
]
D.(ln3,ln2+1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项为正的数列{an}满足 ![]() ,
,
(1)当λ=an+1时,求证:数列{an}是等比数列,并求其公比;
(2)当λ=2时,令 ![]() ,记数列{bn}的前n项和为Sn , 数列{bn}的前n项之积为Tn , 求证:对任意正整数n,2n+1Tn+Sn为定值.
,记数列{bn}的前n项和为Sn , 数列{bn}的前n项之积为Tn , 求证:对任意正整数n,2n+1Tn+Sn为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com