
分析 (1)通过$h'(x)=2-\frac{a^2}{x^2}+\frac{1}{x}$、x=1是函数h(x)的极值点及a>0,可得$a=\sqrt{3}$,再检验即可;
(2)通过分析已知条件等价于对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max.结合当x∈[1,e]时及$g'(x)=1+\frac{1}{x}>0$可知[g(x)]max=g(e)=e+1.
利用$f'(x)=1-\frac{a^2}{x^2}=\frac{{({x+a})({x-a})}}{x^2}$,且x∈[1,e],a>0,分0<a<1、1≤a≤e、a>e三种情况讨论即可.
解答 解:(1)∵$f(x)=x+\frac{a^2}{x}$,g(x)=x+lnx,
∴$h(x)=2x+\frac{a^2}{x}+lnx$,其定义域为(0,+∞),
∴$h'(x)=2-\frac{a^2}{x^2}+\frac{1}{x}$.
∵x=1是函数h(x)的极值点,
∴h′(1)=0,即3-a2=0.
∵a>0,∴$a=\sqrt{3}$.
经检验当$a=\sqrt{3}$时,x=1是函数h(x)的极值点,
∴$a=\sqrt{3}$;
(2)对任意的x1,x2∈[1,e]都有f(x1)≥g(x2)成立等价于
对任意的x1,x2∈[1,e]都有[f(x)]min≥[g(x)]max.
当x∈[1,e]时,$g'(x)=1+\frac{1}{x}>0$.
∴函数g(x)=x+lnx在[1,e]上是增函数.
∴[g(x)]max=g(e)=e+1.
∵$f'(x)=1-\frac{a^2}{x^2}=\frac{{({x+a})({x-a})}}{x^2}$,且x∈[1,e],a>0.
①当0<a<1且x∈[1,e]时,$f'(x)=\frac{{({x+a})({x-a})}}{x^2}>0$,
∴函数$f(x)=x+\frac{a^2}{x}$在[1,e]上是增函数,
∴${[{f(x)}]_{min}}=f(1)=1+{a^2}$.
由1+a2≥e+1,得a≥$\sqrt{e}$,
又0<a<1,∴a不合题意;
②当1≤a≤e时,
若1≤x<a,则$f'(x)=\frac{{({x+a})({x-a})}}{x^2}<0$,
若a<x≤e,则$f'(x)=\frac{{({x+a})({x-a})}}{x^2}>0$.
∴函数$f(x)=x+\frac{a^2}{x}$在[1,a)上是减函数,在(a,e]上是增函数.
∴[f(x)]min=f(a)=2a.
由2a≥e+1,得a≥$\frac{e+1}{2}$,
又1≤a≤e,∴$\frac{e+1}{2}$≤a≤e;
③当a>e且x∈[1,e]时,$f'(x)=\frac{{({x+a})({x-a})}}{x^2}<0$,
∴函数$f(x)=x+\frac{a^2}{x}$在[1,e]上是减函数.
∴${[{f(x)}]_{min}}=f(e)=e+\frac{a^2}{e}$.
由$e+\frac{a^2}{e}$≥e+1,得a≥$\sqrt{e}$,
又a>e,∴a>e;
综上所述:a的取值范围为$[{\frac{e+1}{2},+∞})$.
点评 本题是一道关于导数的综合题,考查极值、最值等基本知识,考查运算求解能力,注意解题方法的积累,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [16,20) | B. | (16,20] | C. | (16,24) | D. | [16,24] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
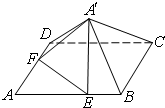 如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2$\sqrt{6}$.
如图,已知正方形ABCD的边长为6,点E,F分别在边AB,AD上,AE=AF=4,现将△AEF沿线段EF折起到△A′EF位置,使得A′C=2$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≤2或m≥4 | B. | -4≤m≤-2 | C. | 2≤m≤4 | D. | 以上皆不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com