
分析 (1)根据定积分求出质点在第1s内的路程,从而求出质点在第1s内的平均速度即可;
(2)求出f′(1)的值,即质点在第1s末的瞬时速度;
(3)令f′(x)=14,求出x的值即可.
解答 解:(1)f(x)=$\frac{2}{3}$x3+x2+2x,f′(x)=2x2+2x+2,
故${∫}_{0}^{1}$($\frac{2}{3}$x3+x2+2x)=($\frac{1}{6}$x4+$\frac{1}{3}$x3+x2)${|}_{0}^{1}$=$\frac{3}{2}$,
故质点在第1s内的平均速度是$\frac{3}{2}$m/s;
(2)根据(1)得:f′(1)=6
质点在第1s末的瞬时速度是6m/s;
(3)由2x2+2x+2=14,解得:x=2,
故经过2s质点的运动速度达到14m/s.
点评 本题考查了瞬时速度,考查导数的应意义,是一道基础题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:选择题
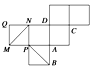 如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为( )
如图是一正方体的表面展开图,MN和PB是两条面对角线,则在正方体中,直线MN与直线PB的位置关系为( )| A. | 相交 | B. | 平行 | C. | 异面 | D. | 重合 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若A∈l,B∈l,且A∈α,B∈α,则l?α | |
| B. | 若直线 a∩b=A,则直线a与直线b能确定一个平面 | |
| C. | 任意三点A、B、C可以确定一个平面 | |
| D. | 若P∈α∩β且α∩β=l,则P∈l |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
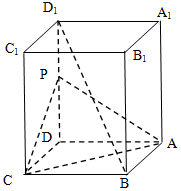 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com