
如图,α⊥β,α∩β=l,A∈α,B∈β,点A在直线l上的射影为A1,点B在直线l上的射影为B1,已知AB=2,AA1=1,BB1=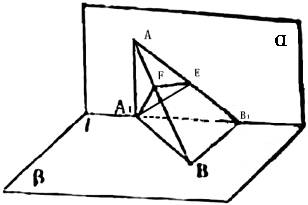 ,求:
,求:
(Ⅰ)直线AB分别与平面α,β所成的角的大小;
(Ⅱ)二面角A1-AB-B1的大小.
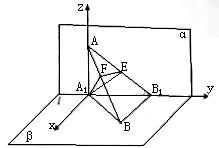
解法一:(Ⅰ)如图,连接A1B,AB1.

∵α⊥β,α∩β=l,AA1⊥l,BB1⊥l, ∴AA1⊥β,BB1⊥α,
则∠BAB1,∠ABA1分别是AB与α和β所成的角.
Rt△BB1A中,BB1=![]() ,AB=2,∴sin∠BAB1=
,AB=2,∴sin∠BAB1=![]() ,
,
∴∠BAB1=45°.
Rt△AA1B中,AA1=1,AB=2,
∴sin∠ABA1=![]() , ∴∠ABA1=30°.
, ∴∠ABA1=30°.
故AB与平面α,β所成的角分别是45°,30°.
(Ⅱ)∵BB1⊥α,
∴平面ABB1⊥α,在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB.
∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=![]() .
.
∴Rt△AA1B1中,AA1=A1B1=1,∴A1E=![]() AB1=
AB1=![]() .
.
在Rt△AA1B中,A1B=![]() .
.
由 AA1·A1B=A1F·AB得
A1F=![]() .
.
∴在Rt△A1EF中,sin∠A1FE=![]() =
=![]() ,
,
∴二面角A1-AB-B1的大小为arcsin![]() .
.
解法二:(Ⅰ)同解法一.
(Ⅱ)如图,建立坐标系,则A1(0,0,0),A(0,0,1),B1(0,1,0),B(![]() ,1,0).
,1,0).

在AB上取一点F(x,y,z),则存在t∈R,使得![]() =t
=t![]() ,
,
即(x,y,z-1)=t(![]() ),
),
∴点F的坐标为(![]() t,t,1-t).
t,t,1-t).
要使 ![]() ,须
,须![]() =0,
=0,
即(![]() ,t,1-t)·(
,t,1-t)·(![]() ,1,-1)=0,2t+t-(1-t)=0,解得t=
,1,-1)=0,2t+t-(1-t)=0,解得t=![]() ,
,
∴点F的坐标为(![]() ),
),
∴![]() (
(![]() ).
).
设E为AB1的中点,则点E的坐标为(0,![]() ).
).
∴![]()
又![]()
∴![]() , ∴∠A1FE为所求二面角的平面角.
, ∴∠A1FE为所求二面角的平面角.
又 cos∠A1FE=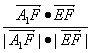


![]()
∴二面角A1-AB-B1的大小为arccos![]() .
.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
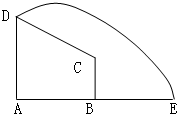 如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=
如图,在直角梯形ABCD中,AD∥BC,DA⊥AB,AD=3,AB=4,BC=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com