
某食品企业一个月内被消费者投诉的次数用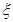 表示,椐统计,随机变量
表示,椐统计,随机变量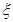 的概率分布如下:
的概率分布如下:
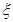 | 0 | 1 | 2 | 3 |
| p | 0.1 | 0.3 | 2a | a |
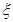 的数学期望;
的数学期望;(1)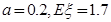 ;(2)
;(2)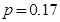 .
.
解析试题分析:(1)由概率分布的性质可求得a,再由求期望的公式即可求得数学期望.
(2) “两个月内共被投诉2次”这个事件包含以下两个事件: “两个月内有一个月被投诉2次,另外一个月被投诉0次”; “两个月内每月均被投诉1次”,这两个事件显然互斥,那么求出这两个事件的概率相加即得.
试题解析:(1)由概率分布的性质有0.1+0.3+2a+a=1,解答a=0.2 2分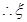 的概率分布为
的概率分布为
4分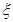
0 1 2 3 P 0.1 0.3 0.4 0.2 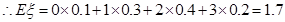 6分
6分
(2)设事件A表示“两个月内共被投诉2次”,事件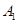 表示“两个月内有一个月被投诉2次,另外一个月被投诉0次”;事件
表示“两个月内有一个月被投诉2次,另外一个月被投诉0次”;事件 表示“两个月内每月均被投诉1次”,这两个事件互斥.
表示“两个月内每月均被投诉1次”,这两个事件互斥.
由题设,一月份与二月份被消费者投诉的次数互不影响,即相互独立,所以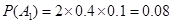 8分
8分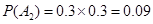 10分
10分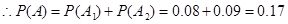
故该企业在这两个月内共被消费者投诉2次的概率为0.17 12分
考点:1、概率分布的性质;2、随机变量的分布列及期望;3、互斥事件与独立事件的概率.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为 ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求出甲、乙两人所付租车费用相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量 ,求
,求 的分布列与数学期望
的分布列与数学期望 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔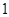 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
(1)根据样品数据,计算甲、乙两个车间产品重量的平均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间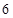 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过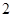 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某旅游推介活动晚会进行嘉宾现场抽奖活动,抽奖规则是:抽奖盒中装有 个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
个大小相同的小球,分别印有“多彩十艺节”和“美丽泉城行”两种标志,摇匀后,参加者每次从盒中同时抽取两个小球,若抽到两个球都印有“多彩十艺节”标志即可获奖.
(I)活动开始后,一位参加者问:盒中有几个“多彩十艺节”球?主持人笑说:我只知道从盒中同时抽两球不都是“美丽泉城行”标志的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(Ⅱ)上面条件下,现有甲、乙、丙、丁四人依次抽奖,抽后放回,另一个人再抽,用 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系? 表示抽得甲班的学生人数,求
表示抽得甲班的学生人数,求 的分布列.
的分布列.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品.现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有7名奥运会志愿者,其中志愿者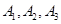 通晓日语,
通晓日语,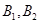 通晓俄语,
通晓俄语,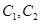 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求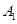 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求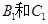 不全被选中的概率.(5分)
不全被选中的概率.(5分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将编号为1,2,3,4的四个小球,分别放入编号为1,2,3,4的四个盒子,每个盒子中有且仅有一个小球.若小球的编号与盒子的编号相同,得1分,否则得0分.记 为四个小球得分总和.
为四个小球得分总和.
(1)求 时的概率;
时的概率;
(2)求 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com