
【题目】下列命题错误的是
A. 三棱锥的四个面可以都是直角三角形;
B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11是一个定值,则S16为定值;
C. ![]() 中,sinA>sinB是
中,sinA>sinB是![]() 的充要条件;
的充要条件;
D. 若双曲线的渐近线互相垂直,则这条双曲线是等轴双曲线.
【答案】B
【解析】
A,找到满足题意的特殊图形即可;B,根据等差数列的性质可得到命题正确;C,根据正弦定理得到大边对大角,进而得到结论;D,设出双曲线方程,求出渐近线方程,通过斜率之积为定值-1,得到a,b的关系.
对于A,三棱锥的四个面可以都是直角三角形正确,如三条侧棱两两垂直,底面是直角三角形,A正确;B. 等差数列{an}的前n项和为Sn(n=1,2,3…),若当首项a1和公差d变化时,a5+a8+a11=3![]() ,则
,则![]() 不一定是一个定值,故B错误;对于C△ABC中,由正弦定理可得
不一定是一个定值,故B错误;对于C△ABC中,由正弦定理可得![]() ,因此sinA>sinBa>bA>B,因此sinA>sinB是A>B的充要条件,正确;D设双曲线的方程为:
,因此sinA>sinBa>bA>B,因此sinA>sinB是A>B的充要条件,正确;D设双曲线的方程为:![]() ,渐近线方程分别为
,渐近线方程分别为![]() ,斜率之积为定值-1,则
,斜率之积为定值-1,则![]() ,故双曲线是等轴双曲线.
,故双曲线是等轴双曲线.
故答案为:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,设![]() ,
,![]() 分别是正方体
分别是正方体![]() 的棱
的棱![]() 上两点,且
上两点,且![]() ,
,![]() ,其中正确的命题为( )
,其中正确的命题为( )
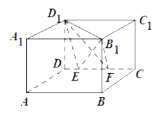
A.三棱锥![]() 的体积为定值
的体积为定值
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.![]() 平面
平面![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年俄罗斯世界杯期间,莫斯科的部分餐厅经营了来自中国的小龙虾,这些小龙虾标有等级代码.为得到小龙虾等级代码数值![]() 与销售单价
与销售单价![]() 之间的关系,经统计得到如下数据:
之间的关系,经统计得到如下数据:
等级代码数值 | 38 | 48 | 58 | 68 | 78 | 88 |
销售单价 | 16.8 | 18.8 | 20.8 | 22.8 | 24 | 25.8 |
(1)已知销售单价![]() 与等级代码数值
与等级代码数值![]() 之间存在线性相关关系,求
之间存在线性相关关系,求![]() 关于
关于![]() 的线性回归方程(系数精确到0.1);
的线性回归方程(系数精确到0.1);
(2)若莫斯科某个餐厅打算从上表的6种等级的中国小龙虾中随机选2种进行促销,记被选中的2种等级代码数值在60以下(不含60)的数量为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:对一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距最小二乘估计分别为:
的斜率和截距最小二乘估计分别为: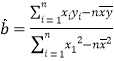 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在单位正![]() 内任取一点P,以PA、PB、PC为边生成
内任取一点P,以PA、PB、PC为边生成![]() .
.
(1)当![]() 分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
分别为锐角三角形、直角三角形、钝角三角形时,求出点P的轨迹.
(2)证明:当![]() 的周长取最小值时,面积取最大值.
的周长取最小值时,面积取最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了坚决打赢新冠状病毒的攻坚战,阻击战,某小区对小区内的![]() 名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取
名居民进行模排,各年龄段男、女生人数如下表.已知在小区的居民中随机抽取![]() 名,抽到
名,抽到![]() 岁~
岁~![]() 岁女居民的概率是
岁女居民的概率是![]() .现用分层抽样的方法在全小区抽取
.现用分层抽样的方法在全小区抽取![]() 名居民,则应在
名居民,则应在![]() 岁以上抽取的女居民人数为( )
岁以上抽取的女居民人数为( )
|
|
| |
女生 |
|
|
|
男生 |
|
|
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在直线![]() 上的圆C经过
上的圆C经过![]() 点,且与直线
点,且与直线![]() 相切.
相切.
(1)求过点P且被圆C截得的弦长等于4的直线方程;
(2)过点P作两条相异的直线分别与圆C交于A,B,若直线PA,PB的倾斜角互补,试判断直线AB与OP的位置关系(O为坐标原点),并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中![]() )
)
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的![]() ,求三所高校的教授的总人数.
,求三所高校的教授的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com