
【题目】已知中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() 的椭圆过点
的椭圆过点![]() .
.
(1)求椭圆方程;
(2)设不过原点O的直线![]() ,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为
,与该椭圆交于P、Q两点,直线OP、OQ的斜率依次为![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据题意列出方程组: 解出即可;(2)联立直线和椭圆得到方程:(4k2+1)x2+8kmx+4m2-4=0,4k=k1+k2=
解出即可;(2)联立直线和椭圆得到方程:(4k2+1)x2+8kmx+4m2-4=0,4k=k1+k2=![]() ,由韦达定理得到表达式,进而得到结果.
,由韦达定理得到表达式,进而得到结果.
(1)设椭圆的方程为![]() +
+![]() =1(a>b>0),则由题意得
=1(a>b>0),则由题意得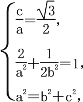 解得a=2,b=1,
解得a=2,b=1,
∴椭圆的方程为![]() +y2=1.
+y2=1.
(2)由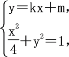 得(4k2+1)x2+8kmx+4m2-4=0,
得(4k2+1)x2+8kmx+4m2-4=0,
令Δ=64k2m2-4(4k2+1)(4m2-4)>0,得m2<4k2+1(*),
∴x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
设P(x1,y1),Q(x2,y2),∴k1=![]() ,k2=
,k2=![]() ,
,
则4k=k1+k2=![]() +
+![]() =
=![]() =
=![]() =2k-
=2k-![]() ,
,
∴m2=![]() ,满足(*)式,故m2=
,满足(*)式,故m2=![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,△ABC中,![]() ,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
,ABED是边长为1的正方形,平面ABED⊥底面ABC,若G,F分别是EC,BD的中点.
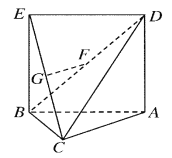
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;
(3)求几何体ADEBC的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知(1+x)+(1+x)2+(1+x)3+…+(1+x)n的展开式中x的系数恰好是数列{an}的前n项和Sn .
(1)求数列{an}的通项公式;
(2)数列{bn}满足 ![]() ,记数列{bn}的前n项和为Tn , 求证:Tn<1.
,记数列{bn}的前n项和为Tn , 求证:Tn<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴,长度单位相同,建立极坐标系,已知圆A的参数方程为 ![]() (其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(Ⅰ)分别写出圆A与圆B的直角坐标方程;
(Ⅱ)判断两圆的位置关系,若两圆相交,求其公共弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若
(a>b>0)的左焦点为F,C与过原点的直线相交于A,B两点,连接AF,BF.若![]() ,
,![]() ,cos ∠ABF=
,cos ∠ABF=![]() ,则C的离心率为( )
,则C的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量分别为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y (单位:万件)与月份x 的关系.模拟函数1:y=ax+ ![]() +c
+c
;模拟函数2:y=mnx+s.
(1)已知4月份的产量为13.7 万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=3sinx﹣πx,命题p:x∈(0, ![]() ),f(x)<0,则( )
),f(x)<0,则( )
A.p是假命题,¬p:?x∈(0, ![]() ),f(x)≥0
),f(x)≥0
B.p是假命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
C.p是真命题,¬p:?x∈(0, ![]() ),f(x)>0
),f(x)>0
D.p是真命题,¬p:?x0∈(0, ![]() ),f(x0)≥0
),f(x0)≥0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司经营一批进价为每件400元的商品,在市场调查时发现,此商品的销售单价x(元)与日销售量y(件)之间的关系如下表所示:
x/元 | 500 | 600 | 700 | 800 | 900 |
y/件 | 10 | 8 | 9 | 6 | 1 |
(1)求y关于x的回归直线方程.
(2)借助回归直线方程,预测销售单价为多少元时,日利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,D是到原点的距离不大于1的点构成的区域,E是满足不等式组 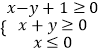 的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
的点(x,y)构成的区域,向D中随机投一点,则所投的点落在E中的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com