
为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人调查,就是否“取消英语听力”的问题,调查统计的结果如下表:
| 应该取消 | 应该保留 | 无所谓 | ||
| 在校学生 | 2100人 | 120人 | y人 | ||
| 社会人士 | 600人 | x人 | z人 |
(1)应在“无所谓”态度抽取72人.
(2)ξ的分布列为:
Eξ=2.ξ 1 2 3 P 


解析试题分析:(1)频率即为概率,所以 =0.05,解得x=60.这样可得持“无所谓”态度的人数,共有3600-2100-120-600-60=720人.分层抽样实质上就是按比例抽样,所以应在“无所谓”态度抽取720×
=0.05,解得x=60.这样可得持“无所谓”态度的人数,共有3600-2100-120-600-60=720人.分层抽样实质上就是按比例抽样,所以应在“无所谓”态度抽取720× =72人.(2)由(1)知持“应该保留”态度的人一共有180人,按比例计算可得在所抽取的6人中,在校学生为
=72人.(2)由(1)知持“应该保留”态度的人一共有180人,按比例计算可得在所抽取的6人中,在校学生为 =4人,社会人士为
=4人,社会人士为 =2人.将这6人平均分成两组,则第一组在校学生人数ξ=1,2,3.这是一个超几何分布,根据超几何分布的概率公式即可得其分布列,进而求得其期望.
=2人.将这6人平均分成两组,则第一组在校学生人数ξ=1,2,3.这是一个超几何分布,根据超几何分布的概率公式即可得其分布列,进而求得其期望.
试题解析:(1)∵抽到持“应该保留”态度的人的概率为0.05,
∴ =0.05,解得x=60. 2分
=0.05,解得x=60. 2分
∴持“无所谓”态度的人数共有3600-2100-120-600-60=720. 4分
∴应在“无所谓”态度抽取720× =72人. 6分
=72人. 6分
(2)由(1)知持“应该保留”态度的一共有180人,
∴ 在所抽取的6人中,在校学生为 =4人,社会人士为
=4人,社会人士为 =2人,
=2人,
于是第一组在校学生人数ξ=1,2,3, 8分
P(ξ=1)= ,P(ξ=2)=
,P(ξ=2)= ,P(ξ=3)=
,P(ξ=3)= ,
,
即ξ的分布列为:
10分ξ 1 2 3 P 


∴ Eξ=1× +2×
+2× +3×
+3× =2. 12分
=2. 12分
考点:1、简单随机抽样;2、古典概型;3、随机变量的分布列及期望.


科目:高中数学 来源: 题型:解答题
甲、乙两名运动员参加“选拔测试赛”,在相同条件下,两人5次测试的成绩(单位:分)记录如下:
甲 86 77 92 72 78
乙 78 82 88 82 95
(1)用茎叶图表示这两组数据;.
(2)现要从中选派一名运动员参加比赛,你认为选派谁参赛更好?说明理由(不用计算);
(3)若从甲、乙两人的5次成绩中各随机抽取一个,求甲的成绩比乙高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在某大学联盟的自主招生考试中,报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如下图所示,本次考试中成绩在 内的记为
内的记为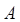 ,其中“语文”科目成绩在
,其中“语文”科目成绩在 内的考生有10人.
内的考生有10人.
(1)求该考场考生数学科目成绩为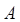 的人数;
的人数;
(2)已知参加本考场测试的考生中,恰有2人的两科成绩均为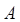 .在至少一科成绩为
.在至少一科成绩为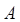 的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为
的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为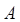 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
| | 喜爱打篮球 | 不喜爱打篮球 | 合计 |
| 男生 | | 5 | |
| 女生 | 10 | | |
| 合计 | | | 50 |
 .
.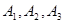 还喜欢打羽毛球,
还喜欢打羽毛球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求 和
和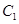 不全被选中的概率.
不全被选中的概率. | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
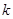 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某学校随机抽取部分新生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学路上所需时间的范围是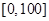 ,样本数据分组为
,样本数据分组为 ,
, ,
, ,
, ,
, .
.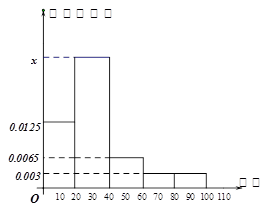
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生可申请在学校住宿,请估计学校1000名新生中有多少名学生可以申请住宿;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| | 喜欢 | 不喜欢 | 合计 |
| 大于40岁 | 20 | 5 | 25 |
| 20岁至40岁 | 10 | 20 | 30 |
| 合计 | 30 | 25 | 55 |
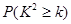 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
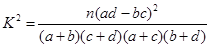 ,其中
,其中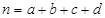 )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位有2000名职工,老年、中年、青年分布在管理、技术开发、营销、生产各部门中,如下表所示:
| 人数 | 管理 | 技术开发 | 营销 | 生产 | 共计 |
| 老年 | 40 | 40 | 40 | 80 | 200 |
| 中年 | 80 | 120 | 160 | 240 | 600 |
| 青年 | 40 | 160 | 280 | 720 | 1 200 |
| 小计 | 160 | 320 | 480 | 1 040 | 2 000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学举行了为期3天的新世纪体育运动会,同时进行全校精神文明擂台赛.为了解这次活动在全校师生中产生的影响,分别在全校500名教职员工、3000名初中生、4000名高中生中作问卷调查,如果要在所有答卷中抽出120份用于评估.
(1)应如何抽取才能得到比较客观的评价结论?
(2)要从3000份初中生的答卷中抽取一个容量为48的样本,如果采用简单随机抽样,应如何操作?
(3)为了从4000份高中生的答卷中抽取一个容量为64的样本,如何使用系统抽样抽取到所需的样本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):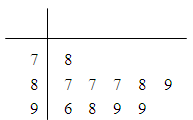
(1)指出这组数据的众数和中位数;
(2)若满意度不低于98分,则评价该教师为“优秀”.求从这10人中随机选取3人,至多有1人评价
该教师是“优秀”的概率;
(3)以这10人的样本数据来估计整个班级的总体数据,若从该班任选3人,记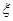 表示抽到评价该教师为
表示抽到评价该教师为
“优秀”的人数,求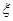 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com