
【题目】在△ABC中,角A,B,C的所对的边分别为a,b,c,且a2+b2=ab+c2 .
(Ⅰ) 求tan(C﹣ ![]() )的值;
)的值;
(Ⅱ) 若c= ![]() ,求S△ABC的最大值.
,求S△ABC的最大值.
【答案】解:(Ⅰ)∵a2+b2=ab+c2 , a2+b2﹣c2=ab,
∴cosC= ![]() =
= ![]() ,
,
∵C为△ABC内角,
∴C= ![]() ,
,
则tan(C﹣ ![]() )=tan(
)=tan( ![]() ﹣
﹣ ![]() )=
)= ![]() =2﹣
=2﹣ ![]() ;
;
(Ⅱ)由ab+3=a2+b2≥2ab,得ab≤3,
∵S△ABC= ![]() absinC=
absinC= ![]() ab,
ab,
∴S△ABC≤ ![]() ,
,
当且仅当a=b= ![]() 时“=”成立,
时“=”成立,
则S△ABC的最大值是 ![]()
【解析】(Ⅰ) 利用余弦定理表示出cosC,将已知等式变形后代入求出cosC的值,确定出C的度数,代入tan(C﹣ ![]() )计算即可求出值;(Ⅱ)把c的值代入已知等式变形,利用基本不等式求出ab的最大值,再由sinC的值,即可求出三角形ABC面积的最大值.
)计算即可求出值;(Ⅱ)把c的值代入已知等式变形,利用基本不等式求出ab的最大值,再由sinC的值,即可求出三角形ABC面积的最大值.
【考点精析】关于本题考查的正弦定理的定义和余弦定理的定义,需要了解正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD,底面ABCD为边长为2对的菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点. 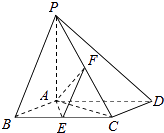
(1)判定AE与PD是否垂直,并说明理由;
(2)若PA=2,求二面角E﹣AF﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 、
、 ![]() 是两个不共线的向量,且
是两个不共线的向量,且 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ).
=(cosβ,sinβ).
(1)求证: ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直;
垂直;
(2)若α∈(﹣ ![]() ,
, ![]() ),β=
),β= ![]() ,且|
,且| ![]() +
+ ![]() |=
|= ![]() ,求sinα.
,求sinα.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,∠AED=90°,且平面ABCD⊥平面ADEF,AF=FE=AB= ![]() AD=2,点G为AC的中点.
AD=2,点G为AC的中点. 
(Ⅰ)求证:平面BAE⊥平面DCE;
(Ⅱ)求三棱锥B﹣AEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ax2﹣(2a+1)x+2lnx(a∈R)
ax2﹣(2a+1)x+2lnx(a∈R)
(1)当a= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)设g(x)=(x2﹣2x)ex , 如果对任意x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD,底面ABCD为正方形,侧面PAD为直角三角形,且PA=PD,面PAD⊥面ABCD,E、F分别为AB、PD的中点. 
(Ⅰ)求证:EF∥面PBC;
(Ⅱ)求证:AP⊥面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|< ![]() ).
). 
(1)求函数f(t)的解析式;
(2)点P第二次到达最高点要多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com