
【题目】今年3月10日湖北武汉某方舱医院“关门大吉”,某省驰援湖北“抗疫”的9名身高各不相同的医护人员站成一排合影留念,庆祝圆满完成“抗疫”任务,若恰好从中间往两边看都依次变低,则身高排第4的医护人员和最高的医护人员相邻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
将身高从低到高的9个人依次编号为1,2,3,4,5,6,7,8,9,则9号定在正中间,两边是四个元素的定序排列,6号与9号分左右两边相邻,与6在同一边的另外3个元素(从1,2,3,4,5种任选3个)定序排列,另一边的四个元素定序排列, 最后根据古典概型的概率公式可得答案.
身高最高
将身高从低到高的9个人依次编号为1,2,3,4,5,6,7,8,9,
则9号必须排在正中间,从其余8个人中任选4人排在9号的左边,剩下的4个人排在9号的右边,有![]() 种,
种,
当排名第四的6号排在最高的9号的左边时,从1,2,3,4,5中任选3个排在6号的左边,其余四个排在9号的右边,有![]() 种,同理当当排名第四的6号排在最高的9号的右边时,也有10种,
种,同理当当排名第四的6号排在最高的9号的右边时,也有10种,
所以身高排名第四的6号与最高的9号相邻的排法有10+10=20种,
所以身高排第4的医护人员和最高的医护人员相邻的概率为![]() .
.
故选:A.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对
,对![]() ∈[0, π],都有
∈[0, π],都有![]() ,满足f(x2)=0的实数x有且只有3个,给出下述四个结论:①满足题目条件的实数x0有且只有1个;②满足题目条件的实数x1有且只有1个;③f(x)在
,满足f(x2)=0的实数x有且只有3个,给出下述四个结论:①满足题目条件的实数x0有且只有1个;②满足题目条件的实数x1有且只有1个;③f(x)在![]() 上单调递增;④
上单调递增;④![]() 的取值范围是
的取值范围是![]() ;其中所有正确结论的编号是( )
;其中所有正确结论的编号是( )
A.①③B.②④C.①②④D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了严格监控某种零件的一条生产线的生产过程,某企业每天从该生产线上随机抽取10000个零件,并测量其内径(单位:![]() ).根据长期生产经验,认为这条生产线正常状态下生产的零件的内径
).根据长期生产经验,认为这条生产线正常状态下生产的零件的内径![]() 服从正态分布
服从正态分布![]() .如果加工的零件内径小于
.如果加工的零件内径小于![]() 或大于
或大于![]() 均为不合格品,其余为合格品.
均为不合格品,其余为合格品.
(1)假设生产状态正常,请估计一天内抽取的10000个零件中不合格品的个数约为多少;
(2)若生产的某件产品为合格品则该件产品盈利;若生产的某件产品为不合格品则该件产品亏损.已知每件产品的利润![]() (单位:元)与零件的内径
(单位:元)与零件的内径![]() 有如下关系:
有如下关系: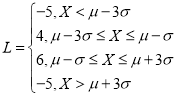 .求该企业一天从生产线上随机抽取10000个零件的平均利润.
.求该企业一天从生产线上随机抽取10000个零件的平均利润.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,有
,有![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P ABC中,PA⊥平面ABC,![]() Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为
Q是BC边上的一个动点,且直线PQ与面ABC所成角的最大值为![]() 则该三棱锥外接球的表面积为( )
则该三棱锥外接球的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD-A1B1C1D1中,E、F、G分别为AA1、BC、C1D1的中点,现有下面三个结论:①△EFG为正三角形;②异面直线A1G与C1F所成角为60°;③AC∥平面EFG.其中所有正确结论的编号是( )
A.①B.②③C.①②D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解该校学生“停课不停学”的网络学习效率,随机抽查了高一年级100位学生的某次数学成绩,得到如图所示的频率分布直方图:
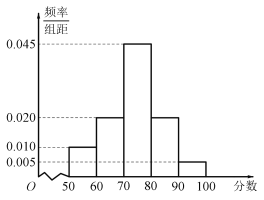
(1)估计这100位学生的数学成绩的平均值![]() .(同一组中的数据用该组区间的中点值代表);
.(同一组中的数据用该组区间的中点值代表);
(2)根据整个年级的数学成绩,可以认为学生的数学成绩![]() 近似地服从正态分布
近似地服从正态分布![]() 经计算,(1)问中样本标准差
经计算,(1)问中样本标准差![]() 的近似值为10.用样本平均数
的近似值为10.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
的估计值,现任抽取一位学生,求他的数学成绩恰在64分到94分之间的概率.
参考数据:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]()
(3)该年级1班的数学老师为了能每天督促学生的网络学习,提高学生每天的作业质量及学习数学的积极性,特意在微信上设计了一个每日作业小程序,每当学生提交的作业获得优秀时,就有机会参与一次小程序中“玩游戏,得奖励积分”的活动,开学后可根据获得积分的多少领取老师相应的小奖品.小程序页面上有一列方格,共15格,刚开始有只小兔子在第1格,每点一下游戏的开始按钮,小兔子就沿着方格跳一下,每次跳1格或跳2格,概率均为![]() ,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第
,依次点击游戏的开始按钮,直到小兔子跳到第14格(奖励0分)或第15格(奖励5分)时,游戏结束,每天的积分自动累加,设小兔子跳到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求
是等比数列,并求![]() 的值.(获胜的概率)
的值.(获胜的概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD﹣A1B1C1D1中,底面ABCD是矩形,A1D与AD1交于点E,AA1=AD=2AB=4.
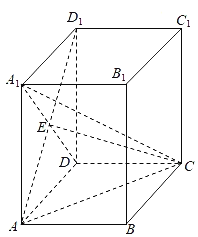
(1)证明:AE⊥平面ECD.
(2)求点C1到平面AEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,已知四边形AA1C1C为矩形,AA1=6,AB=AC=4,∠BAC=∠BAA1=60°,∠A1AC的角平分线AD交CC1于D.
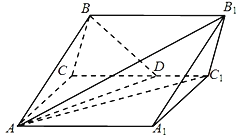
(1)求证:平面BAD⊥平面AA1C1C;
(2)求二面角A﹣B1C1﹣A1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产口罩、防护服、消毒水等防疫物品,保障抗疫一线医疗物资供应,在国际社会上赢得一片赞誉.我国某口罩生产企业在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,该企业质检人员从所生产的口罩中随机抽取了100个,将其质量指标值分成以下六组:![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,得到如下频率分布直方图.
,得到如下频率分布直方图.
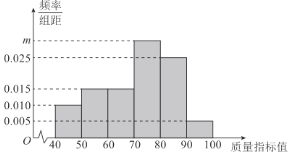
(1)求出直方图中![]() 的值;
的值;
(2)利用样本估计总体的思想,估计该企业所生产的口罩的质量指标值的平均数和中位数(同一组中的数据用该组区间中点值作代表,中位数精确到0.01);
(3)现规定:质量指标值小于70的口罩为二等品,质量指标值不小于70的口罩为一等品.利用分层抽样的方法从该企业所抽取的100个口罩中抽出5个口罩,并从中再随机抽取2个作进一步的质量分析,试求这2个口罩中恰好有1个口罩为一等品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com