[题目]如图.点P在正方形ABCD所在平面外.PD⊥平面ABCD.PD=AD.则PA与BD所成角的度数为( ) 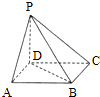A.30°B.45°C.60°D.90° 题目和参考答案——青夏教育精英家教网—

【题目】如图，点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，则PA与BD所成角的度数为（）
A.30°
B.45°
C.60°
D.90°

【答案】C
【解析】解：如图，以D为坐标原点，DA所在直线为x轴，DC所在线为y轴，DP所在线为z轴，建立空间坐标系， ∵点P在正方形ABCD所在平面外，PD⊥平面ABCD，PD=AD，令PD=AD=1
∴A（1，0，0），P（0，0，1），B（1，1，0），D（0，0，0）
∴ =（1，0，﹣1）， =（﹣1，﹣1，0）
∴cosθ= =
故两向量夹角的余弦值为，即两直线PA与BD所成角的度数为60°．
故选C
本题求解宜用向量法来做，以D为坐标原点，建立空间坐标系，求出两直线的方向向量，利用数量积公式求夹角即可

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】甲、乙两名同学在五次考试中数学成绩统计用茎叶图如表示如图2所示，则甲的平均成绩比乙的平均成绩（填高、低、相等）；甲成绩的方差比乙成绩的方差（填大、小）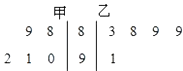

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知a，b，c分别为△ABC三个内角A，B，C所对的边长，且acosB﹣bcosA= c．
（1）求的值；
（2）若A=60°，求的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】定义：若函数f（x）对于其定义域内的某一数x0 ，有 f（x0）=x0 ，则称x0是f （x）的一个不动点．已知函数f（x）=ax2+（b+1）x+b﹣1 （a≠0）．
（1）当a=1，b=﹣2时，求函数f（x）的不动点；
（2）若对任意的实数b，函数f（x）恒有两个不动点，求a的取值范围；
（3）在（2）的条件下，若y=f（x）图象上两个点A，B的横坐标是函数f（x）的不动点，且A，B两点关于直线y=kx+ 对称，求b的最小值．