
【题目】已知f(x)是定义在R上的奇函数,且f(x+2)=f(x﹣2);当0≤x≤1时,f(x)= ![]() ,则f(1)+f(2)+f(3)+…+f等于( )
,则f(1)+f(2)+f(3)+…+f等于( )
A.﹣1
B.0
C.1
D.2
【答案】C
【解析】解:由f(x+2)=f(x﹣2)得f(x+4)=f(x),则函数是周期为4的周期函数,
∵f(x)是定义在R上的奇函数,
∴当0≤x≤1时,f(x)= ![]() ,则f(0)=0,f(1)=1,
,则f(0)=0,f(1)=1,
当x=0时,f(2)=f(﹣2)=﹣f(2),则f(2)=0,
f(3)=f(3﹣4)=f(﹣1)=﹣f(1)=﹣1,
f(4)=f(0)=0,
则在一个周期内f(1)+f(2)+f(3)+f(4)=1+0﹣1+0=0,
则f(1)+f(2)+f(3)+…+f=504[f(1)+f(2)+f(3)+f(4)]+f
=f=f(1)=1,
故选:C.
【考点精析】本题主要考查了函数奇偶性的性质的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】下列四个判断: ①某校高三一班和高三二班的人数分别是m,n,某次测试数学平均分分别是a,b,则这两个班的数学平均分为 ![]() ;
;
②10名工人某天生产同一零件的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则有c>a>b;
③从总体中抽取的样本为 ![]() ,则回归直线
,则回归直线 ![]() 必过点(
必过点( ![]() )
)
④已知ξ服从正态分布N(0,σ2),且P(﹣2≤ξ≤0)=4,则P(ξ>2)=0.2
其中正确的个数有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数 ![]() ,其中a>0.设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.则b的最大值为( )
,其中a>0.设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.则b的最大值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kex﹣x2(其中k∈R,e是自然对数的底数).
(Ⅰ)若k<0,试判断函数f(x)在区间(0,+∞)上的单调性;
(Ⅱ)若k=2,当x∈(0,+∞)时,试比较f(x)与2的大小;
(Ⅲ)若函数f(x)有两个极值点x1 , x2(x1<x2),求k的取值范围,并证明0<f(x1)<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中,a1=1,且a1 , a2 , a4+2成等比数列.
(1)求数列{an}的通项公式及其前n项和Sn;
(2)设 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(3+x)﹣log2(3﹣x),
(1)求函数f(x)的定义域,并判断函数f(x)的奇偶性;
(2)已知f(sinα)=1,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aexlnx+ ![]() ,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
,曲线y=f(x)在点(1,f(1))处得切线方程为y=e(x﹣1)+2.
(Ⅰ)求a、b;
(Ⅱ)证明:f(x)>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地电影院为了了解当地影迷对快要上映的一部电影的票价的看法,进行了一次调研,得到了票价x(单位:元)与渴望观影人数y(单位:万人)的结果如下表:
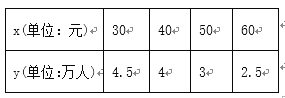
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;
(2)根据(1)中求出的线性回归方程,若票价定为70元,预测该电影院渴望观影人数.附:回归直线的斜率和截距的最小二乘法估计公式分别为: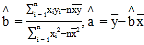
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com