
【题目】已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上.
上.
(1)求![]() 的边
的边![]() 所在的直线方程;
所在的直线方程;
(2)求![]() 的面积最小值,并求出此时点
的面积最小值,并求出此时点![]() 的坐标;
的坐标;
(3)若![]() 为线段
为线段![]() 上的任意一点,求
上的任意一点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 的面积最小值为3,此时
的面积最小值为3,此时![]() 点坐标为
点坐标为![]() .(3)
.(3)![]()
【解析】
(1)直接由两点式可得直线方程;
(2) 设点![]() 坐标为
坐标为![]() ,利用点到直线的距离求出点
,利用点到直线的距离求出点![]() 到
到![]() 的距离,再根据二次函数知识求出这个距离的最大值,以及取得最大值的条件,再根据面积公式可求得面积的最大值,根据取得最大值的条件可求得点
的距离,再根据二次函数知识求出这个距离的最大值,以及取得最大值的条件,再根据面积公式可求得面积的最大值,根据取得最大值的条件可求得点![]() 的坐标;
的坐标;
(3)根据 ![]() 的几何意义,转化为
的几何意义,转化为![]() ,
,![]() 的斜率,结合图象可得答案.
的斜率,结合图象可得答案.
解:(1)∵![]() ,
,![]() ,
,
∴直线![]() 的方程为
的方程为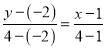 ,即
,即![]() .
.
(2)设点![]() 坐标为
坐标为![]() ,
,
如图所示:
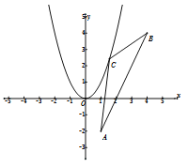
则点![]() 到直线
到直线![]() 距离
距离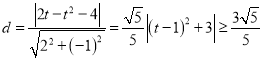 ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() 的面积最小值为3.当且仅当
的面积最小值为3.当且仅当![]() 时等号成立,此时
时等号成立,此时![]() 点坐标为
点坐标为![]() .
.
(3)∵![]() 为线段
为线段![]() 上任意一点,
上任意一点,
∴![]() 的几何意义为坐标原点
的几何意义为坐标原点![]() 与线段
与线段![]() 上的点所确定直线的斜率,
上的点所确定直线的斜率,
即![]() 的几何意义为当直线
的几何意义为当直线![]() 与线段
与线段![]() 有交点时,直线
有交点时,直线![]() 的斜率,
的斜率,
如图所示:
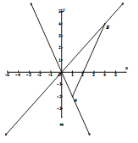
![]() ,
,![]() ,
,
∴![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别为内角A,B,C的对边,且asin B=-bsin![]() .
.
(1)求A;
(2)若△ABC的面积S=![]() c2,求sin C的值.
c2,求sin C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (
(![]() 为参数),以直角坐标系原点为极点,x轴非负半轴为极轴并取相同的单位长度建立极坐标系,
为参数),以直角坐标系原点为极点,x轴非负半轴为极轴并取相同的单位长度建立极坐标系,
(1)求曲线C的极坐标方程,并说明其表示什么轨迹;
(2)若直线l的极坐标方程为![]() ,求曲线C上的点到直线l的最大距离.
,求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程是
的方程是![]() ,双曲线
,双曲线![]() 的左右焦点分别为
的左右焦点分别为![]() 的左右顶点,而
的左右顶点,而![]() 的左右顶点分别是
的左右顶点分别是![]() 的左右焦点.
的左右焦点.
(1)求双曲线![]() 的方程;
的方程;
(2)若直线![]() 与双曲线
与双曲线![]() 恒有两个不同的交点,且
恒有两个不同的交点,且![]() 与
与![]() 的两个交点A和B满足
的两个交点A和B满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是正方形
是正方形![]() 所在平面外一点,
所在平面外一点,![]() 在面
在面![]() 上的投影为
上的投影为![]() ,
,![]() ,
,![]() ,
,![]() ,有以下四个命题:
,有以下四个命题:
(1)![]() 面
面![]() ;
;
(2)![]() 为
为![]() 中点,且
中点,且![]() ;
;
(3)以![]() ,
,![]() 作为邻边的平行四边形面积是32;
作为邻边的平行四边形面积是32;
(4)![]() 的内切球半径为
的内切球半径为![]() .
.
其中正确命题的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有户籍人口60万,经统计,该县60岁及以上、百岁以下的人口占比![]() ,百岁及以上老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
,百岁及以上老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
年龄段(岁) |
|
|
|
|
人数(人) | 125 | 75 | 25 | 5 |
(1)从样本中70岁及以上老人中,采用分层抽样的方法抽取21人,进一步了解他们的生活状况,则80岁及以上老人应抽多少人?
(2)从(1)中所抽取的80岁及以上老人中,再随机抽取2人,求抽到90岁及以上老人的概率;
(3)该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神,制定如下老年人生活补贴措施,由省、市、县三级财政分级拨款:
①本县户籍60岁及以上居民,按城乡居民养老保险实施办法每月领取55元基本养老金;
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴;
(a)百岁及以上老年人,每人每月发放345元的生活补贴;
(b)90岁及以上、百岁以下老年人,每人每月发放200元的生活补贴;
(c)80岁及以上、90岁以下老年人,每人每月发放100元的生活补贴.
试估计政府执行此项补贴措施的年度预算.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关命题的说法错误的是( )
A.若p∨q为假命题,则p、q均为假命题
B.“x=1”是“x2﹣3x+2=0”的充分不必要条件
C.命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
D.对于命题p:x≥0,2x=3,则¬P:x<0,2x≠3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com