
【题目】已知椭圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,一动圆在
,一动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,此动圆的圆心轨迹为曲线
相外切,此动圆的圆心轨迹为曲线![]() ,椭圆
,椭圆![]() 与曲线
与曲线![]() 有相同的焦点.
有相同的焦点.
(1)求曲线![]() 的方程;
的方程;
(2)设曲线![]() 与椭圆
与椭圆![]() 相交于第一象限点
相交于第一象限点![]() ,且
,且![]() ,求椭圆
,求椭圆![]() 的标准方程;
的标准方程;
(3)在(2)的条件下,如果椭圆![]() 的左顶点为
的左顶点为![]() ,过
,过![]() 且垂直于
且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 与直线
与直线![]() :
:![]() 分别交于
分别交于![]() ,
,![]() 两点,证明:四边形
两点,证明:四边形![]() 的对角线的交点是椭圆
的对角线的交点是椭圆![]() 的右顶点.
的右顶点.
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)设动圆圆心的坐标为![]() ,
,![]() ,计算化简得到答案.
,计算化简得到答案.
(2)计算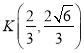 ,则
,则![]() ,得到答案.
,得到答案.
(3)计算![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为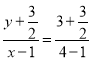 ,令
,令![]() ,得
,得![]() ,得到答案.
,得到答案.
(1)设动圆圆心的坐标为![]() ,因为动圆在
,因为动圆在![]() 轴右侧与
轴右侧与![]() 轴相切,同时与圆
轴相切,同时与圆![]() 相外切,所以
相外切,所以![]() ,所以
,所以![]() ,化简整理得
,化简整理得![]() ,
,
曲线![]() 的方程为
的方程为![]() .
.
(2)依题意,![]() ,
,![]() ,可得
,可得![]() ,故
,故![]() 点坐标为
点坐标为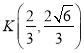 ,
,
椭圆的另一焦点为![]() ,
,
由两点间的距离可得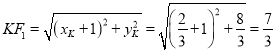 ,
,
又由椭圆的定义得![]() ,
,![]() .
.
所以![]() ,所以椭圆
,所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(3)由(2)知![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
根据椭圆的对称性,当直线![]() 轴时,四边形
轴时,四边形![]() 是等腰梯形,对角线的交点在
是等腰梯形,对角线的交点在![]() 轴上,此时直线
轴上,此时直线![]() 的方程为
的方程为![]() ,
,
由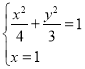 ,
,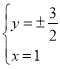 ,不妨取
,不妨取![]() ,
,![]() ,
,
故直线![]() 的方程为
的方程为![]() ,将
,将![]() 代入得
代入得![]() ,
,
所以直线![]() 的方程为
的方程为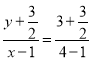 ,令
,令![]() ,得
,得![]() ,
,
即直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,此时恰好为椭圆的右顶点.
,此时恰好为椭圆的右顶点.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,
两点,![]() 为坐标原点.
为坐标原点.
(1)若直线![]() 过椭圆
过椭圆![]() 的右焦点
的右焦点![]() ,求
,求![]() 的面积;
的面积;
(2)若![]() ,试问椭圆
,试问椭圆![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
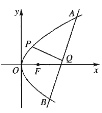
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线上一点,且
是抛物线上一点,且![]() ,直线
,直线![]() 过定点(4,0),与抛物线
过定点(4,0),与抛物线![]() 交于
交于![]() 两点,点
两点,点![]() 在直线
在直线![]() 上的射影是
上的射影是![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
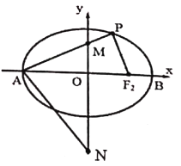
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,左右顶点分别为
,左右顶点分别为![]() ,
,![]() ,右焦点为
,右焦点为![]() ,
,![]() 为椭圆上异于
为椭圆上异于![]() ,
,![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 轴交于
轴交于![]() 点,过点
点,过点![]() 作
作![]() 的平行线交
的平行线交![]() 轴与点
轴与点![]() ,试探究是否存在定点
,试探究是否存在定点![]() ,使得以
,使得以![]() 为直径的圆恒过定点
为直径的圆恒过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
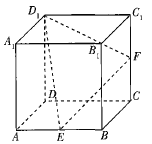
【题目】如图,在棱长为12的正方体![]() 中,已知E,F分别为棱AB,
中,已知E,F分别为棱AB,![]() 的中点,若过点
的中点,若过点![]() ,E,F的平面截正方体
,E,F的平面截正方体![]() 所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面
所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面![]() ,ABCD的交线所成角的余弦值为________.
,ABCD的交线所成角的余弦值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且四个顶点构成的四边形的面积是
,且四个顶点构成的四边形的面积是![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 经过点
经过点![]() ,且不垂直于
,且不垂直于![]() 轴,直线
轴,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为
为![]() 的中点,直线
的中点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() 是坐标原点),求四边形
是坐标原点),求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纹样是中国传统文化的重要组成部分,它既代表着中华民族的悠久历史、社会的发展进步,也是世界文化艺术宝库中的巨大财富.小楠从小就对纹样艺术有浓厚的兴趣.收集了如下9枚纹样微章,其中4枚凤纹徽章,5枚龙纹微章.小楠从9枚徽章中任取3枚,则其中至少有一枚凤纹徽章的概率为( ).

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com