解:(1)由已知,得a
1=S
1=
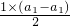
=0,∴S
n=
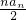
,
则有S
n+1=
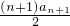
,
∴2(S
n+1-S
n)=(n+1)a
n+1-na
n,即(n-1)a
n+1=na
n n∈N*,
∴na
n+2=(n+1)a
n+1,
两式相减得,2a
n+1=a
n+2+a
n n∈N*,
即a
n+1-a
n+1=a
n+1-a
n n∈N*,
故数列{a
n}是等差数列.
又a
1=0,a
2=a,∴a
n=(n-1)a.
(2)若a=2,则a
n=2(n-1),∴S
n=n(n-1).
由
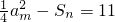
,得n
2-n+11=(m-1)
2,即4(m-1)
2-(2n-1)
2=43,
∴(2m+2n-3)(2m-2n-1)=43.
∵43是质数,2m+2n-3>2m-2n-1,2m+2n-3>0,
∴
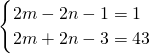
,解得m=12,n=11.
(3)由a
n+b≤p,得a(n-1)+b≤p.
若a<0,则n≥
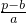
+1,不合题意,舍去;
若a>0,则n≤
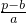
+1.∵不等式a
n+b≤p成立的最大正整数解为3p-2,
∴3p-2≤
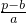
+1<3p-1,
即2a-b<(3a-1)p≤3a-b,对任意正整数p都成立.
∴3a-1=0,解得a=

,
此时,

-b<0≤1-b,解得

<b≤1.
故存在实数a、b满足条件,a与b的取值范围是a=

,

<b≤1.
分析:(1)利用数列的项与前n项和的关系,将条件转化为数列的项之间的关系,判定数列为特征数列,再求通项公式;
(2)利用(1)的结论,求出m、n满足的关系,分析求解即可;
(3)根据条件a
n+b≤p求出n满足的条件,再根据满足a
n+b≤p的最大项始终为3P-2,转化为不等式的恒成立问题,分析求解即可.
点评:本题考查了等差数列的通项公式,数列的项与前n项和之间的关系及数列的综合问题.

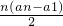 (n∈N*).
(n∈N*).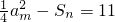 ,求m、n的值;
,求m、n的值;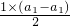 =0,∴Sn=
=0,∴Sn=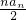 ,
,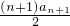 ,
,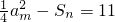 ,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,
,得n2-n+11=(m-1)2,即4(m-1)2-(2n-1)2=43,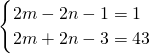 ,解得m=12,n=11.
,解得m=12,n=11.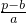 +1,不合题意,舍去;
+1,不合题意,舍去; 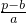 +1.∵不等式an+b≤p成立的最大正整数解为3p-2,
+1.∵不等式an+b≤p成立的最大正整数解为3p-2,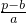 +1<3p-1,
+1<3p-1, ,
, -b<0≤1-b,解得
-b<0≤1-b,解得 <b≤1.
<b≤1. ,
, <b≤1.
<b≤1.

 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案