
【题目】已知A(0,1),B(0,﹣1),M(﹣1,0),动点P为曲线C上任意一点,直线PA,PB的斜率之积为![]() ,动直线l与曲线C相交于不同两点Q(x1,y1),R(x2,y2),其中y1>0,y2>0且满足
,动直线l与曲线C相交于不同两点Q(x1,y1),R(x2,y2),其中y1>0,y2>0且满足![]() .
.
(1)求曲线C的方程;
(2)若直线l与x轴相交于一点N,求N点坐标.
【答案】(1)![]() (x≠0);(2)N(﹣2,0)
(x≠0);(2)N(﹣2,0)
【解析】
(1)由已知及求轨迹方程的步骤可得到曲线C的轨迹方程;
(2)设直线l的方程为y=k(x﹣m),联立直线方程与椭圆方程,化为关于x的一元二次方程,由已知可得kMQ+kMR=0,结合根与系数的关系代入即可解出N点坐标.
(1)动点P为曲线C上任意一点,直线PA,PB的斜率之积为![]() ,设动点P(x,y),x≠0;
,设动点P(x,y),x≠0;
则有:kPAkPB![]()
![]() ,化简可得:
,化简可得:![]() ,x≠0.
,x≠0.
故曲线C的方程为:![]() (x≠0);
(x≠0);
(2)设点N的坐标为(m,0).依题意,直线l的斜率存在且不为0,设为k(k≠0),
则直线l的方程y=k(x﹣m),将y=k(x﹣m)代入方程![]() y2=1(x≠0).
y2=1(x≠0).
得(2k2+1)x2﹣4k2mx+2(k2m2﹣1)=0.
则△=(﹣4k2m)2﹣8(2k2+1)(k2m2﹣1)=8(2k2﹣k2m2+1)>0,
动直线与曲线C相交于不同两点Q(x1,y1),R(x2,y2),其中y1>0,y2>0,
x1+x2![]() ,x1x2
,x1x2![]() ,且满足
,且满足![]() ,即
,即![]() ,
,
如图,

![]() ,
,![]() ,
,
则![]() ,故kMQ+kMR=0,
,故kMQ+kMR=0,
即![]() ,
,
化简得:![]() ,
,
即![]() ,整理得m+2=0,即m=﹣2.
,整理得m+2=0,即m=﹣2.
故点N的坐标为(﹣2,0).


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中a是常数).
(其中a是常数).
(1)求过点![]() 与曲线
与曲线![]() 相切的直线方程;
相切的直线方程;
(2)是否存在![]() 的实数,使得只有唯一的正数a,当
的实数,使得只有唯一的正数a,当![]() 时不等式
时不等式![]() 恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x![]() )+2sin(
)+2sin(![]() )sin(
)sin(![]() x).
x).
(Ⅰ)求f(x)的单调递增区间;
(Ⅱ)求函数y=f(x)的对称轴方程,并求函数f(x)在区间[![]() ,
,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点P(3,﹣4)作圆(x﹣1)2+y2=2的切线,切点分别为A,B,则直线AB的方程为( )
A.x+2y﹣2=0B.x﹣2y﹣1=0C.x﹣2y﹣2=0D.x+2y+2=0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P–ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且![]() .
.
(Ⅰ)求证:CD⊥平面PAD;
(Ⅱ)求二面角F–AE–P的余弦值;
(Ⅲ)设点G在PB上,且![]() .判断直线AG是否在平面AEF内,说明理由.
.判断直线AG是否在平面AEF内,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证
时,求证![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
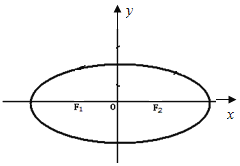
【题目】如图,F1(﹣2,0),F2(2,0)是椭圆C:![]() 的两个焦点,M是椭圆C上的一点,当MF1⊥F1F2时,有|MF2|=3|MF1|.
的两个焦点,M是椭圆C上的一点,当MF1⊥F1F2时,有|MF2|=3|MF1|.
(1)求椭圆C的标准方程;
(2)过点P(0,3)作直线l与轨迹C交于不同两点A,B,使△OAB的面积为![]() (其中O为坐标原点),问同样的直线l共有几条?并说明理由.
(其中O为坐标原点),问同样的直线l共有几条?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】吸烟有害健康,小明为了帮助爸爸戒烟,在爸爸包里放一个小盒子,里面随机摆放三支香烟和三支跟香烟外形完全一样的“戒烟口香糖”,并且和爸爸约定,每次想吸烟时,从盒子里任取一支,若取到口香糖则吃一支口香糖,不吸烟;若取到香烟,则吸一支烟,不吃口香糖,假设每次香烟和口香糖被取到的可能性相同,则“口香糖吃完时还剩2支香烟”的概率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com