
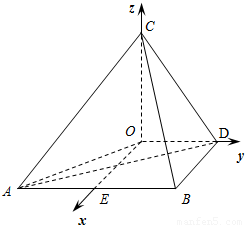
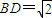 ,沿BD将△BCD折起,使二面角A-BD-C是大小为锐角α的二面角,设C在平面ABD上的射影为O.
,沿BD将△BCD折起,使二面角A-BD-C是大小为锐角α的二面角,设C在平面ABD上的射影为O.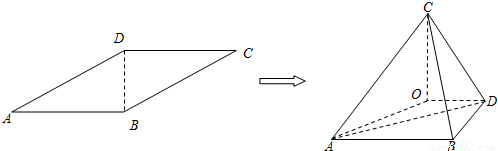
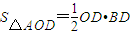 ,OC⊥平面ABDO,利用三棱锥的体积计算公式和正弦函数的单调性即可得出;
,OC⊥平面ABDO,利用三棱锥的体积计算公式和正弦函数的单调性即可得出;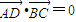 ,即可得出.
,即可得出.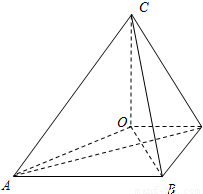 解:(1)由题知OD为CD在平面ABD上的射影,
解:(1)由题知OD为CD在平面ABD上的射影,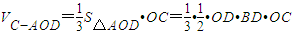
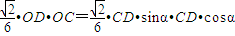 =
=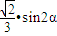
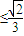 ,
,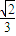 .
. 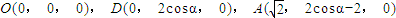 ,
,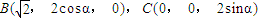 ,
,
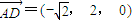 ,
,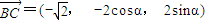 ,
,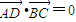 ,
,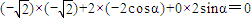 ,
,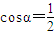 ,又α为锐角,∴α=60°.
,又α为锐角,∴α=60°.

科目:高中数学 来源: 题型:
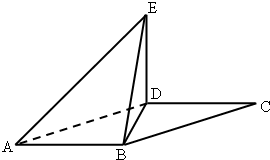 如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.
如图,平行四边形ABCD中,∠DAB=60°,AB=2,AD=4将△CBD沿BD折起到△EBD的位置,使平面EDB⊥平面ABD.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若
如图,平行四边形ABCD中,E,F分别是BC,DC的中点,G为交点,若| AB |
| a |
| AD |
| b |
| a |
| b |
| CG |
| 1 |
| 3 |
| a |
| b |
| 1 |
| 3 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则
(2012•枣庄一模)如图,平行四边形ABCD中,点E是边BC(靠近点B)的三等分点,F是AB(靠近点A)的三等分点,P是AE与DF的交点,则| AP |
| AB |
| AD |
| AP |
| 3 |
| 10 |
| AB |
| 1 |
| 10 |
| AD |
| AP |
| 3 |
| 10 |
| AB |
| 1 |
| 10 |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
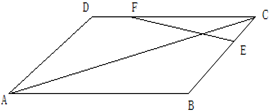 如图,平行四边形ABCD中,
如图,平行四边形ABCD中,| AB |
| a |
| AD |
| b |
| CE |
| 1 |
| 3 |
| CB |
| CF |
| 2 |
| 3 |
| CD |
| a |
| b |
| EF |
| a |
| b |
| EF |
| AC |
| FE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com