练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．用二分法研究函数f（x）=x3-2x-1的理念时，若零点所在的初始区间为（1，2），则下一个有解区间为（　　）
    A．（1，2）B．（1.75，2）C．（1.5，2）D．（1，1.5）

    分析 构造函数f（x）=x3-2x-1，确定f（1），f（2），f（1.5）的符号，根据零点存在定理，即可得到结论．

    解答 解：设函数f（x）=x3-2x-1，
    ∵f（1）=-2＜0，f（2）=3＞0，f（1.5）=-$\frac{5}{8}$＜0，
    ∴下一个有根区间是（1.5，2），
    故选：C．

    点评 本题考查二分法，考查零点存在定理，考查学生的计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．已知向量$\overrightarrow{a}$=（1，0），$\overrightarrow{b}$=（m，1），且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{4}$．
    （1）求|$\overrightarrow{a}$-2$\overrightarrow{b}$|；
    （2）若（$\overrightarrow{a}$+λ$\overrightarrow{b}$）与$\overrightarrow{b}$垂直，求实数λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．已知圆M：（x-a）2+y2=4（a＞0）与圆N：x2+（y-1）2=1外切，则直线x-y-$\sqrt{2}$=0被圆M截得线段的长度为（　　）
    A．1B．$\sqrt{3}$C．2D．2$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．下列说法正确的是（　　）
    A．“若a＞1，则a2＞1”的否命题是“若a＞1，则a2≤1”
    B．在△ABC中，“A＞B”是“sin2A＞sin2B”必要不充分条件
    C．“若tanα$≠\sqrt{3}$，则$α≠\frac{π}{3}$”是真命题
    D．?x0∈（-∞，0）使得3${\;}^{{x}_{0}}$＜4${\;}^{{x}_{0}}$成立

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

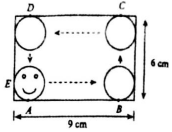    13．有一个电动玩具，它有一个9×6的长方形（单位：cm）和一个半径为1cm的小圆盘（盘中娃娃脸），他们的连接点为A，E，打开电源，小圆盘沿着长方形内壁，从点A出发不停地滚动（无滑动），如图所示，若此时某人向该长方形盘投掷一枚飞镖，则能射中小圆盘运行区域内的概率为$\frac{40+π}{54}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．要得到y=sin$\frac{x}{2}$的图象，只需将y=cos（$\frac{x}{2}$-$\frac{π}{4}$）的图象上的所有点（　　）
    A．向右平移$\frac{π}{2}$B．向左平移$\frac{π}{2}$C．向左平移$\frac{π}{4}$D．向右平移$\frac{π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）定义在区间（-1，1）内，对于任意的x，y∈（-1，1）有f（x）+f（y）=f（$\frac{x+y}{1+xy}$），且当x＜0时，f（x）＞0．
    （1）判断这样的函数是否具有奇偶性和单调性，并加以证明；
    （2）若f（-$\frac{1}{2}$）=1，求方程f（x）+$\frac{1}{2}$=0的解．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知P，Q为椭圆$\frac{x^2}{2}+{y^2}=1$上的两点，满足PF2⊥QF2，其中F1，F2分别为左右焦点．
    （1）求$|\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}|$的最小值；
    （2）若$（\overrightarrow{P{F_1}}+\overrightarrow{P{F_2}}）⊥（\overrightarrow{Q{F_1}}+\overrightarrow{Q{F_2}}）$，设直线PQ的斜率为k，求k2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．“?x∈[1，2]，x2-a≥0“是真命题，则实数a的最大值为1．

    查看答案和解析>>

    同步练习册答案