Question

已知直线（t为参数）经过椭圆（为参数）的左焦点F.

（Ⅰ）求m的值；

（Ⅱ）设直线l与椭圆C交于A、B两点，求|FA|·|FB|的最大值和最小值.

 

Answer 1

【答案】

（Ⅰ）－1; （Ⅱ）当sinα＝0时，|FA|·|FB|取最大值3；当sinα＝±1时，|FA|·|FB|取最小值．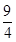

【解析】

试题分析：（Ⅰ）利用公式将椭圆C的参数方程化为普通方程，求出左焦点F代入直线方程求解m；（Ⅱ）将l的参数方程代入椭圆C的普通方程，借助t的几何含义求解|FA|·|FB|的最大值和最小值.

试题解析：（Ⅰ）将椭圆C的参数方程化为普通方程，得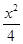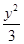＋＝1．

a＝2，b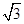＝，c＝1，则点F坐标为(－1，0)．

l是经过点(m，0)的直线，故m＝－1．

（Ⅱ）将l的参数方程代入椭圆C的普通方程，并整理，得

(3cos²α＋4sin²α)t²－6tcosα－9＝0．

设点A，B在直线参数方程中对应的参数分别为t₁，t₂，则

|FA|·|FB|＝|t₁t₂|＝＝．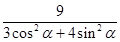

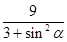当sinα＝0时，|FA|·|FB|取最大值3；

当sinα＝±1时，|FA|·|FB|取最小值．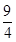

考点：1.参数方程；2.参数t的几何含义.