
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
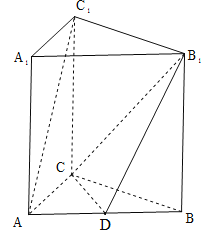
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的正弦值.
的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)连接![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,利用中位线定理得出
,利用中位线定理得出![]() ,再利用线面平行的判定定理可得出结论;
,再利用线面平行的判定定理可得出结论;
(Ⅱ)以![]() 为坐标原点,分别以射线
为坐标原点,分别以射线![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立空间直角坐标系,利用空间向量法以及同角三角函数的基本关系可求得二面角
轴的正方向建立空间直角坐标系,利用空间向量法以及同角三角函数的基本关系可求得二面角![]() 的正弦值.
的正弦值.
(Ⅰ)连接![]() ,设
,设![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,
由题可知四边形![]() 为矩形,所以点
为矩形,所以点![]() 为
为![]() 的中点.
的中点.
又因为![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(Ⅱ)由题可知,![]() ,所以
,所以![]() .
.
又因为![]() 平面
平面![]() ,所以可以
,所以可以![]() 为坐标原点,分别以射线
为坐标原点,分别以射线![]() 、
、![]() 、
、![]() 的方向为
的方向为![]() 、
、![]() 、
、![]() 轴的正方向建立如图所示的空间直角坐标系.
轴的正方向建立如图所示的空间直角坐标系.

则![]() ,
, ,
,![]() ,
,![]() .
.
所以 ,
,![]() ,
, ,
, .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
则 ,令
,令![]() ,可得
,可得![]() .
.
同理可得平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以 ,
,
设二面角![]() 的大小为
的大小为![]() ,则
,则![]() .
.
因此,二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】从某地区随机抽测120名成年女子的血清总蛋白含量(单位:![]() ),由测量结果得如图频数分布表:
),由测量结果得如图频数分布表:
(1)①仔细观察表中数据,算出该样本平均数![]() ______;
______;
②由表格可以认为,该地区成年女子的血清总蛋白含量Z服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本标准差s.经计算,该样本标准差
近似为样本标准差s.经计算,该样本标准差![]() .
.
医学上,Z过高或过低都为异常,Z的正常值范围通常取关于![]() 对称的区间
对称的区间![]() ,且Z位于该区间的概率为
,且Z位于该区间的概率为![]() ,试用该样本估计该地区血清总蛋白正常值范围.
,试用该样本估计该地区血清总蛋白正常值范围.
120名成年女人的血清总蛋白含量的频数分布表 | |||
分组 | 频数f | 区间中点值x |
|
| 2 | 65 | 130 |
| 8 | 67 | 536 |
| 12 | 69 | 828 |
| 15 | 71 | 1065 |
| 25 | 73 | 1825 |
| 24 | 75 | 1800 |
| 16 | 77 | 1232 |
| 10 | 79 | 790 |
| 7 | 81 | 567 |
| 1 | 83 | 83 |
合计 | 120 | 8856 | |
(2)结合(1)中的正常值范围,若该地区有5名成年女子检测血清总蛋白含量,测得数据分别为83.2,80,73,59.5,77,从中随机抽取2名女子,设血清总蛋白含量不在正常值范围的人数为X,求X的分布列和数学期望.
附:若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.直线
上.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为坐标原点,延长线段
为坐标原点,延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求出此时直线
能否为平行四边形?若能,求出此时直线![]() 的方程,若不能,说明理由.
的方程,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“四”“校”“联”“考”四个字,有放回地从中任取一个小球,取到“联”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“四”“校”“联”“考”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:13 24 12 32 43 14 24 32 31 21 23 13 32 21 24 42 13 32 23 34据此估计,直到第二次就停止的概率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在多面体![]() 中,四边形
中,四边形![]() 是正方形,平面
是正方形,平面![]() 平面
平面![]() ,
,![]() .
.
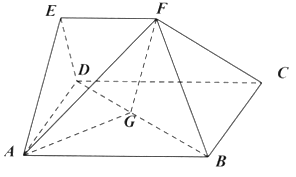
(1)求证:![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成的锐二面角的大小为
所成的锐二面角的大小为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
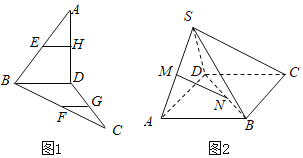
【题目】(1)如图(1)已知E,F,G,H为空间四边形ABCD的边AB,BC,CD,DA上的点,且EH![]() FG.求证:EH
FG.求证:EH![]() BD.
BD.
(2)如图(2):S是平行四边形ABCD平面外一点,M,N分别是SA,BD上的点,且![]() ,求证:MN
,求证:MN![]() 平面SBC.
平面SBC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com