已知圆C:x2+y2-6x-4y+4=0,直线l1被圆所截得的弦的中点为P(5,3).
(1)求直线l1的方程;
(2)若直线l2:x+y+b=0与圆C相交于两个不同的点,求b的取值范围.
【答案】
分析:(1)将圆C方程化为标准方程,找出圆心坐标与半径r,根据垂径定理得到直线CP与直线l
1垂直,根据直线CP的斜率求出直线l
1的斜率,确定出直线l
1的方程即可;
(2)联立圆的方程与直线l
2方程,消去y得到关于x的一元二次方程,根据直线与圆相交于不同的两个点,得到方程有两个不相等的实数根,即根的判别式大于0,即可求出b的范围.
解答:解:(1)由圆C:x
2+y
2-6x-4y+4=0,得(x-3)
2+(y-2)
2=9,
∴圆心C(3,2),半径为3,
由垂径定理知:直线l
1⊥直线CP,
∵直线CP的斜率k
CP=

=

,
∴直线l
1的斜率k
l1=-

=-2,
则直线l
1的方程为y-3=-2(x-5),即2x+y-13=0;
(2)由题意知方程组

有两组解,
由方程组消去y得2x
2+2(b-1)x+b
2+4b+4=0,该方程应有两个不同的解,
∴△=[2(b-1)]
2-8(b
2+4b+4)>0,化简得b
2+10b+7<0,
由b
2+10b+7=0,解得:b=-5±3
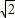
,
∴b
2+10b+7<0解得:-5-3
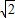
<b<-5+3

,
则b的取值范围是(-5-3

,-5+3
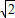
).
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,直线与圆的位置关系由d与r的大小来判断,当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.

 =
= ,
, =-2,
=-2, 有两组解,
有两组解,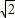 ,
,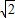 <b<-5+3
<b<-5+3 ,
, ,-5+3
,-5+3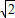 ).
).

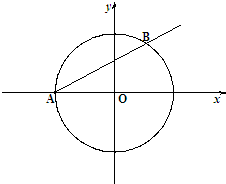 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.