Question

【题目】 山东省《体育高考方案》于2012年2月份公布，方案要求以学校为单位进行体育测试，某校对高三1班同学按照高考测试项目按百分制进行了预备测试，并对50分以上的成绩进行统计，其频率分布直方图如图所示，若90~100分数段的人数为2人.

（Ⅰ）请估计一下这组数据的平均数M；

（Ⅱ）现根据初赛成绩从第一组和第五组（从低分段到高分段依次为第一组、第二组、…、第五组）中任意选出两人，形成一个小组.若选出的两人成绩差大于20，则称这两人为“帮扶组”，试求选出的两人为“帮扶组”的概率.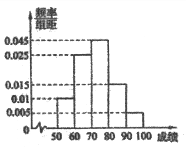

Answer 1

【答案】（Ⅰ）73；（Ⅱ）选出的两人为“帮扶组”的概率为.

【解析】

本试题主要考查了概率的运算和统计图的运用．

（1）由由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05，然后利用平均值公式，可知这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)

（2）中利用90~100分数段的人数为2人，频率为0.05；得到总参赛人数为40，然后得到0~60分数段的人数为40×0.1=4人，第五组中有2人，这样可以得到基本事件空间为15种，然后利用其中两人成绩差大于20的选法有：（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），（A4，B1），（A4，B2）共8种，得到概率值

解：(Ⅰ)由频率分布直方图可知:50~60分的频率为0.1, 60~70分的频率为0.25, 70~80分的频率为0.45, 80~90分的频率为0.15, 90~100分的频率为0.05； ……………2分

∴这组数据的平均数M=55×0.1+65×0.25+75×0.45+85×0.15+95×0.05=73(分)…4分

(Ⅱ)∵90~100分数段的人数为2人，频率为0.05；

∴参加测试的总人数为=40人，……………………………………5分

∴50~60分数段的人数为40×0.1=4人， …………………………6分

设第一组50~60分数段的同学为A1，A2，A3，A4；第五组90~100分数段的同学为B1，B2

则从中选出两人的选法有：（A1，A2），（A1，A3），（A1，A4），（A1，B1），（A1，B2），（A2，A3），（A2，A4），（A2，B1），（A2，B2），（A3，A4），（A3，B1），（A3，B2），（A4，B1），（A4，B2），（B1，B2），共15种；其中两人成绩差大于20的选法有：（A1，B1），（A1，B2），（A2，B1），（A2，B2），（A3，B1），（A3，B2），（A4，B1），（A4，B2）共8种 …………………………11分

则选出的两人为“帮扶组”的概率为