
【题目】已知等比数列![]() 的公比
的公比![]() ,前n项和为
,前n项和为![]() .若
.若![]() ,且
,且![]() 是
是![]() 与
与![]() 的等差中项.
的等差中项.
(1)求![]() ;
;
(2)数列![]() 满足
满足![]() ,
,![]() ,求数列
,求数列![]() 的前2019项和;
的前2019项和;
(3)设![]() ,问数列
,问数列![]() 中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,以![]() 为概率的事件是( )
为概率的事件是( )
A. 恰有1件一等品 B. 至少有一件一等品
C. 至多有一件一等品 D. 都不是一等品
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长是短轴长的
的长轴长是短轴长的![]() 倍,且过点
倍,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若![]() 的顶点
的顶点![]() 、
、![]() 在椭圆上,
在椭圆上, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,
, ![]() 所在的直线斜率为
所在的直线斜率为![]() ,若
,若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆过定点![]() ,且在
,且在![]() 轴上截得线段
轴上截得线段![]() 的长为 4,直线
的长为 4,直线![]() 交
交![]() 轴于点
轴于点![]() .
.
(1)求动圆圆心的轨迹![]() 的方程;
的方程;
(2)直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 两点,分别以
两点,分别以![]() 为切点作轨迹
为切点作轨迹![]() 的切线交于点
的切线交于点![]() ,若
,若![]() .试判断实数
.试判断实数![]() 所满足的条件,并说明理由.
所满足的条件,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
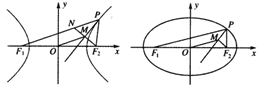
【题目】如图,P是双曲线![]() (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且![]() .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=![]() |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆![]() (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且![]() ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线![]() 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,
满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 0.16 | |
70.5~80.5 | 10 | |
80.5~90.5 | 16 | 0.32 |
90.5~100.5 | ||
合计 | 50 |
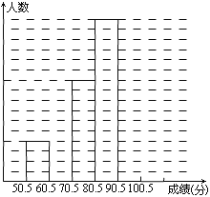
(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
(Ⅱ)补全频数条形图;
(Ⅲ)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】编号分别为![]() 的16名篮球运动员在某次训练比赛中的得分记录如下:
的16名篮球运动员在某次训练比赛中的得分记录如下:
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 |
运动员编号 |
|
|
|
|
|
|
|
|
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(1)将得分在对应区间内的人数填入相应的空格:
区间 | [10,20) | [20,30) | [30,40] |
人数 |
(2)从得分在区间[20,30)内的运动员中随机抽取2人.
(ⅰ)用运动员编号列出所有可能的抽取结果;
(ⅱ)求这2人得分之和大于50的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com