
| A. | $\sqrt{3}f({\frac{π}{4}})>\sqrt{2}f({\frac{π}{3}})$ | B. | $\sqrt{2}f({\frac{π}{6}})>f({\frac{π}{4}})$ | C. | $\sqrt{3}f({\frac{π}{6}})<f({\frac{π}{3}})$ | D. | $f(1)<2f({\frac{π}{6}})sin1$ |
分析 设g(x)=$\frac{f(x)}{sinx}$,根据已知可得g(x)在$({0,\frac{π}{2}})$上递增,故g($\frac{π}{6}$)<g($\frac{π}{3}$),代入整理可得答案.
解答 解:设g(x)=$\frac{f(x)}{sinx}$,
则g′(x)=$\frac{f′(x)•sinx-cosx•f(x)}{{sin}^{2}x}$,
∵cosx•f(x)<f'(x)•sinx在$({0,\frac{π}{2}})$上恒成立,
∴g′(x)>0在$({0,\frac{π}{2}})$上恒成立,
所以g(x)在$({0,\frac{π}{2}})$上递增,
所以g($\frac{π}{6}$)<g($\frac{π}{3}$),
即$\frac{f(\frac{π}{6})}{sin\frac{π}{6}}$<$\frac{f(\frac{π}{3})}{sin\frac{π}{3}}$,
整理得$\sqrt{3}f({\frac{π}{6}})<f({\frac{π}{3}})$,
故选C.
点评 本题考查了利用导数研究函数的单调性,考查了学生的发散思维能力,本题解答的关键是根据给出的条件cosx•f(x)<f'(x)•sinx进行联想,构造函数g(x)=$\frac{f(x)}{sinx}$.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2e3 | B. | $2{e^{\frac{3}{2}}}$或2e3 | C. | $2{e^{\frac{3}{2}}}$ | D. | $2{e^{\frac{3}{2}}}$或2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | asinθ<bsinθ | B. | absinθ<basinθ | ||
| C. | alogbsinθ<blogasinθ | D. | logasinθ<logbsinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
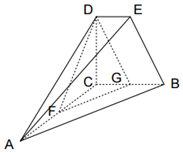 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com