
【题目】某航运公司用300万元买回客船一艘,此船投入营运后,毎月需开支燃油费、维修费、员工工资,已知每月燃油费7000元,第![]() 个月的维修费和工资支出为
个月的维修费和工资支出为![]() 元.
元.
(1)设月平均消耗为![]() 元,求
元,求![]() 与
与![]() (月)的函数关系;
(月)的函数关系;
(2)投入营运第几个月,成本最低?(月平均消耗最小)
(3)若第一年纯收入50万元(已扣除消耗),以后每年纯收入以5%递减,则多少年后可收回成本?
【答案】(1)![]() ;(2)投入第
;(2)投入第![]() 个月,成本最低;
个月,成本最低;
(3)7年后收回成本.
【解析】
(1)先求出购船费和所有支出的和,然后把购船费和所有支出费用平摊到每一个月,即可求得平均消耗![]() 与
与![]() (月)的函数关系;
(月)的函数关系;
(2)利用基本不等式可得最值,从而求出此时![]() 的值,即可求解;
的值,即可求解;
(3)假设![]() 年后可收回成本,则收入是首项为50,公比为0.95的等比数列,然后建立收入大于成本的不等式,即可求解.
年后可收回成本,则收入是首项为50,公比为0.95的等比数列,然后建立收入大于成本的不等式,即可求解.
(1)购船费和所有支出费为
![]()
![]() 元,
元,
所以月平均消耗![]() ,
,
即月平均消耗为![]() 与
与![]() 的函数关系
的函数关系![]() .
.
(2)由(1)![]() ,
,
当且仅当![]() ,即
,即![]() 时等号成立,
时等号成立,
所以当投入营运100个月时,营运成本最低.
(3)假设![]() 年后可收回成本,则收入为:
年后可收回成本,则收入为:
![]() ,
,
解得![]() 时满足条件,
时满足条件,![]() 时不满足条件,
时不满足条件,
故7年后可收回成本.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以![]() ,
,![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,再以
,再以![]() 和
和![]() 的中点
的中点![]() 为顶点作正三角形
为顶点作正三角形![]() ,
,![]() ,如此继续下去.有如下结论:
,如此继续下去.有如下结论:

①所作的正三角形的边长构成公比为![]() 的等比数列;
的等比数列;
②每一个正三角形都有一个顶点在直线![]() 上;
上;
③第六个正三角形的不在第五个正三角形边上的顶点![]() 的坐标是
的坐标是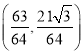 ;
;
④第![]() 个正三角形的不在第
个正三角形的不在第![]() 个正三角形边上的顶点
个正三角形边上的顶点![]() 的横坐标是
的横坐标是![]() ,则
,则![]() .
.
其中正确结论的序号是___________.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过![]() 米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(1)把房屋总造价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知0<m<2,动点M到两定点F1(﹣m,0),F2(m,0)的距离之和为4,设点M的轨迹为曲线C,若曲线C过点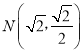 .
.
(1)求m的值以及曲线C的方程;
(2)过定点![]() 且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
且斜率不为零的直线l与曲线C交于A,B两点.证明:以AB为直径的圆过曲线C的右顶点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点S( -2,0) ,T(2,0),动点P为平面上一个动点,且直线SP、TP的斜率之积为![]() .
.
(1)求动点P的轨迹E的方程;
(2)设点B为轨迹E与y轴正半轴的交点,是否存在直线l,使得l交轨迹E于M,N两点,且F(1,0)恰是△BMN的垂心?若存在,求l的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com