
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
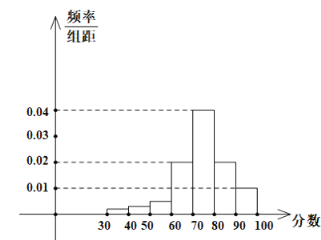
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
【答案】(1)![]() 人(2)
人(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)根据样本总人数100人,中男生有55人,则可算出女生45人.再根据总人数是400人,按样本中的女生人数与样本总人数的比例即可估算出的估计总体中女生人数.
(2)由表可用![]() 减去及格人数的概率得到不及格人数的概率.
减去及格人数的概率得到不及格人数的概率.
(3)设“样本中“良好”或“优秀””为事件B,则![]() ,根据二项分布列出频率分布列,计算数学期望
,根据二项分布列出频率分布列,计算数学期望
解:(1)∵样本中男生有55人,则女生45人
∴估计总体中女生人数![]() 人
人
(2)设“不及格”为事件A,则“及格”为事件![]()
∴![]()
(3)设“样本中“良好”或“优秀””为事件B,则![]()
依题意可知:![]()
![]() ,
,![]()
![]()
所以,X的分布列为
X | 0 | 1 | 2 | 3 |
P | 0.343 | 0.441 | 0.189 | 0.027 |
![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]()
(1)若“![]() x∈A,使得x∈B”为真命题,求m的取值范围;
x∈A,使得x∈B”为真命题,求m的取值范围;
(2)是否存在实数m,使“x∈A”是“X∈B”必要不充分条件,若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经调查统计,网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的![]() 三种商品有购买意向.该淘宝小店推出买一种送5元优惠券的活动.已知某网民购买
三种商品有购买意向.该淘宝小店推出买一种送5元优惠券的活动.已知某网民购买![]() 商品的概率分别为
商品的概率分别为![]() ,
,![]() ,
,![]() ,至少购买一种的概率为
,至少购买一种的概率为![]() ,最多购买两种的概率为
,最多购买两种的概率为![]() .假设该网民是否购买这三种商品相互独立.
.假设该网民是否购买这三种商品相互独立.
(1)求该网民分别购买![]() 两种商品的概率;
两种商品的概率;
(2)用随机变量![]() 表示该网民购买商品所享受的优惠券钱数,求
表示该网民购买商品所享受的优惠券钱数,求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=![]() (a≠0).
(a≠0).
(1)当a=-1,b=0时,求函数f (x)的极值;
(2)当b=1时,若函数f (x)没有零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出![]() 吨该商品可获利润
吨该商品可获利润![]() 万元,未售出的商品,每
万元,未售出的商品,每![]() 吨亏损
吨亏损![]() 万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了
万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了![]() 吨该商品.现以
吨该商品.现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
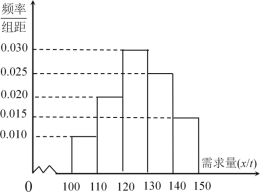
(1)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(2)根据直方图估计利润![]() 不少于57万元的概率;
不少于57万元的概率;
(3)根据频率分布直方图,估计一个销售季度内市场需求量![]() 的平均数与中位数的大小(保留到小数点后一位).
的平均数与中位数的大小(保留到小数点后一位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题甲:对任意实数![]() ,不等式
,不等式![]() 恒成立;命题乙:已知
恒成立;命题乙:已知![]() 满足
满足![]() ,且
,且![]() 恒成立.
恒成立.
(1)分别求出甲乙为真命题时,实数![]() 的取值范围;
的取值范围;
(2)求实数![]() 的取值范围,使命题甲乙中有且只有一个真命题.
的取值范围,使命题甲乙中有且只有一个真命题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感市旅游局为了了解双峰山景点在大众中的熟知度,从年龄在15~65岁的人群中随机抽取![]() 人进行问卷调查,把这
人进行问卷调查,把这![]() 人按年龄分成5组:第一组
人按年龄分成5组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,得到的样本的频率分布直方图如图:
,得到的样本的频率分布直方图如图:
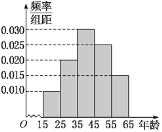
调查问题是“双峰山国家森林公园是几![]() 级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
级旅游景点?”每组中回答正确的人数及回答正确的人数占本组的频率的统计结果如下表.
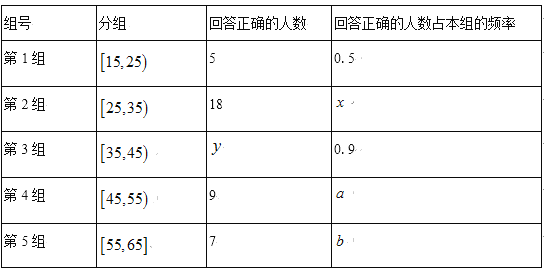
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人;
(3)在(2)抽取的6人中随机抽取2人,求所抽取的两人来自不同年龄组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就是越高,具体浮动情况如下表:
交强险浮动因素和浮动费率比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮10% |
| 上两个年度未发生有责任道路交通事故 | 下浮20% |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
某机构为了 某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这60辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(1)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家的一辆该品牌车在第四年续保时的费用,求
为某同学家的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至多有一辆事故车的概率;
②若该销售商一次购进100辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com