对于函数
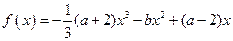
。
(1)若
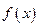
在

处取得极值,且
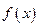
的图像上每一点的切线的斜率均不超过
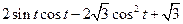
试求实数
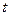
的取值范围;
(2)若
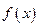
为实数集R上的单调函数,设点P的坐标为
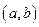
,试求出点P的轨迹所形成的图形的面积S。
(1)

(2)轨迹所围成的图形的面积为

(1)由

,则

因为

处取得极值,所以

的两个根


因为
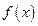
的图像上每一点的切线的斜率不超过
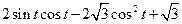
所以
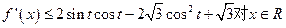
恒成立,
而

,其最大值为1.
故


(2)当

时,由
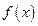
在R上单调,知
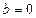
当
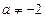
时,由
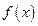
在R上单调
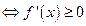
恒成立,或者
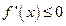
恒成立.
∵

,

可得
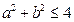
从而知满足条件的点
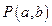
在直角坐标平面
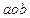
上形成的轨迹所围成的图形的面积为

练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
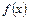
的导函数
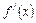
满足
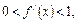
常数
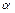
为方程
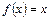
的实数根
(1)若函数
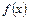
的定义域为I,对任意
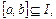
存在
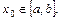
使等式
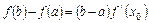
成立。 求证:方程
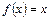
不存在异于
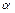
的实数根。
(2)求证:当
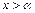
时,总有
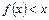
成立。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
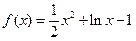
.
(1)求函数
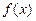
在区间
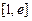
(
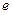
为自然对数的底)上的最大值和最小值;
(2)求证:在区间
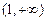
上,函数
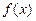
的图象在函数
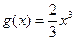
的图象的下方;
(3)求证:
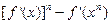
≥
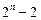
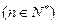
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(文科做)已知函数

(
b、
c为常数).
(1) 若
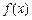
在

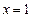
和
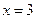
处取得极值,试求
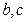
的值;
(2) 若
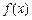
在
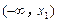
、
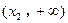
上单调递增,且在
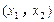
上单调递减,又满足
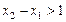
,求证:
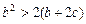
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
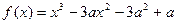
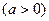
(1)求函数
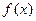
的单调区间;
(2)曲线
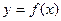
在点
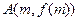
和
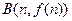
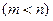
处的切线都与
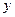
轴垂直,若曲线
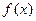
在区间
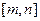
上与
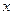
轴相交,求实数
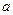
的取值范围;
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
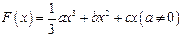
且
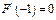
(1)若
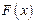
在
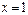
取得极小值-2,求函数
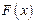
的单调区间
(2)令
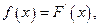
若
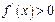
的解集为A,且
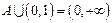
,求
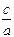
的范围
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
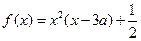
(
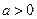
,
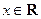
).
(Ⅰ)求函数
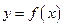
的极值;

(Ⅱ)若函数
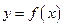
有三个不同的零点,求实数
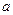
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
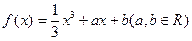
在
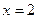
处取得的极小值是
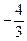
.
(1)求
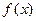
的单调递增区间;
(2)若
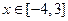
时,有
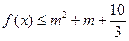
恒成立,求实数
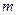
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求下列各函数的导数:
(1)y=
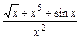
;
(2)y=(x+1)(x+2)(x+3);
(3)y=-sin
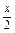
(1-2cos
2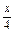
);
(4)y=
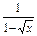
+
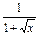
.
查看答案和解析>>

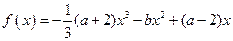 。
。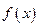 在
在 处取得极值,且
处取得极值,且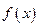 的图像上每一点的切线的斜率均不超过
的图像上每一点的切线的斜率均不超过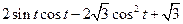 试求实数
试求实数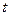 的取值范围;
的取值范围;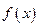 为实数集R上的单调函数,设点P的坐标为
为实数集R上的单调函数,设点P的坐标为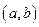 ,试求出点P的轨迹所形成的图形的面积S。
,试求出点P的轨迹所形成的图形的面积S。 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案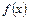 的导函数
的导函数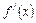 满足
满足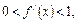 常数
常数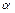 为方程
为方程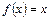
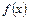 的定义域为I,对任意
的定义域为I,对任意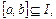 存在
存在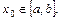 使等式
使等式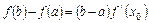 成立。 求证:方程
成立。 求证:方程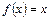 不存在异于
不存在异于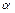 的实数根。
的实数根。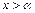 时,总有
时,总有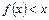 成立。
成立。