
甲、乙两地相距400公里,汽车从甲地匀速行驶到乙地,速度不得超过c公里/小时(c是正常数).已知汽车每小时的运输成本(以元为单位)由可变部分t(元)和固定部分a(a>0)(元)组成.可变部分与速度v(单位:公里/小时)的平方成正比,且知以60公里/小时的速度行驶时,可变部分成本为900元.
(1)写出全程运输成本y与速度v之间的函数解析式;
(2)为了使全程运输成本y最小,汽车应以多大的速度行驶?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 1 |
| 19200 |
| 1 |
| 160 |
查看答案和解析>>
科目:高中数学 来源:2011年《龙门亮剑》高三数学(理科)一轮复习:第2章第10节(人教AB通用)(解析版) 题型:解答题
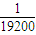 v4-
v4-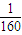 v3+15v,
v3+15v,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 19200 |
| 1 |
| 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:
甲乙两地相距400千米,汽车从甲地匀速行驶到乙地,速度不得超过100千米/小时,已知该汽车每小时的运输成本P(元)关于速度![]()
![]() (千米/小时)的函数关系是
(千米/小时)的函数关系是![]() ,
,
(Ⅰ)求全程运输成本Q(元)关于速度![]() 的函数关系式;
的函数关系式;
(Ⅱ)为使全程运输成本最少,汽车应以多大速度行驶?并求此时运输成本的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com