
【题目】设x>0,求证:1+x+x2+…+xn≥(2n+1)xn
【答案】证明:一:当x≥1时1≤x≤x2≤…≤xn ,
由排序原理:顺序和≥反序和,得
1·1+x·x+x2·x2+…+xn·xn
≥1·xn+x·xn-1+…+xn-1·x+xn·1,
即1+x2+x4+…+x2n≥(n+1)xn.①
又因为x , x2 , …,xn , 1为序列1,x , x2 , …,xn的一个排列,于是再次由排序原理:乱序和≥反序和,得
1·x+x·x2+…+xn-1·xn+xn·1≥1·xn+x·xn-1+…+xn-1·x+xn·1,
得x+x3+…+x2n-1+xn≥(n+1)xn.②
将①和②相加得
1+x+x2+…+xn≥(2n+1)xn.
二:当0<x<1时,1>x>x2>…>xn ,
但①②仍然成立,于是③也成立.
综合一、二,证毕.
【解析】考查排序不等式的应用.解答本题需要注意:题目中只给出了x>0,但对于x≥1,x<1没有明确,因此需要进行分类讨论.
【考点精析】解答此题的关键在于理解排序不等式的相关知识,掌握排序不等式(排序原理):设![]() 为两组实数.
为两组实数.![]() 是
是![]() 的任一排列,则
的任一排列,则![]()
![]() (反序和
(反序和![]() 乱序和
乱序和![]() 顺序和)当且仅当
顺序和)当且仅当![]() 或
或![]() 时,反序和等于顺序和.
时,反序和等于顺序和.


科目:高中数学 来源: 题型:
【题目】已知直线 ![]() ,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
,方程x2+y2﹣2mx﹣2y+m+3=0表示圆.
(Ⅰ)求实数m的取值范围;
(Ⅱ)当m=﹣2时,试判断直线l与该圆的位置关系,若相交,求出相应弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位打字员在两台电脑上各自输入A,B两种类型的文件的部分文字才能使这两类文件成为成品.已知A文件需要甲输入0.5小时,乙输入0.2小时;B文件需要甲输入0.3小时,乙输入0.6小时.在一个工作日中,甲至多只能输入6小时,乙至多只能输入8小时,A文件每份的利润为60元,B文件每份的利润为80元,则甲、乙两位打字员在一个工作日内获得的最大利润是元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx﹣cosx)2+ ![]() sin(2x+
sin(2x+ ![]() )(x∈R).
)(x∈R).
(1)求函数f(x)的递减区间;
(2)若f(α)= ![]() ,α∈(
,α∈( ![]() ,
, ![]() ),求cos(2α+
),求cos(2α+ ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年至2016年新开楼盘的平均销售价格y(单位:千元/平米)的统计数据如表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售价格y | 3 | 3.4 | 3.7 | 4.5 | 4.9 | 5.3 | 6 |
(1)求y关于x的线性回归方程;
(2)利用(Ⅰ)中的回归方程,分析2010年至2016年该市新开楼盘平均销售价格的变化情况,并预测该市2018年新开楼盘的平均销售价格.
附:参考数据及公式: ![]() ,
, 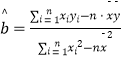 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以 ![]() 为概率的事件是( )
为概率的事件是( )
A.都不是一等品
B.恰有一件一等品
C.至少有一件一等品
D.至多一件一等品
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com