
【题目】如图1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分别延长两腰交于点
,分别延长两腰交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一点,将
上的一点,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2所示.
,如图2所示.
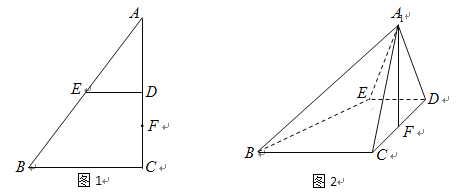
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的表面积.
的表面积.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)先利用直角三角形和线线平行的性质得到线线垂直,再利用线面垂直的判定定理和性质得到线面垂直和线线垂直;(2)分析四棱锥的各面的形状,利用相关面积公式进行求解.
详解:(1)因为∠C=90°,即AC⊥BC,且DE∥BC,

所以DE⊥AC,则DE⊥DC,DE⊥DA1,
又因为DC∩DA1=D,所以DE⊥平面A1DC.
因为A1F平面A1DC,所以DE⊥A1F.
又因为A1F⊥CD,CD∩DE=D,所以A1F⊥平面BCDE,
又因为BE 平面BCDE,所以A1F⊥BE.
(2)由已知DE∥BC,且DE=![]() BC,得D,E分别为AC,AB的中点,
BC,得D,E分别为AC,AB的中点,
在Rt△ABC中,![]() ,则A1E=EB=5,A1D=DC=4,
,则A1E=EB=5,A1D=DC=4,
则梯形BCDE的面积S1=![]() ×(6+3)×4=18,
×(6+3)×4=18,
四棱锥A1—BCDE的体积为V=![]() ×18×A1F=12
×18×A1F=12![]() ,即A1F=2
,即A1F=2![]() ,
,
在Rt△A1DF中,![]() ,即F是CD的中点,
,即F是CD的中点,
所以A1C=A1D=4,
因为DE∥BC,DE⊥平面A1DC,
所以BC⊥平面A1DC,所以BC⊥A1C,所以![]() ,
,
在等腰△A1BE中,底边A1B上的高为![]() ,
,
所以四棱锥A1—BCDE的表面积为S=S1+![]() +
+![]() +
+![]() +
+![]()
=18+![]() ×3×4+
×3×4+![]() ×4×2
×4×2![]() +
+![]() ×6×4+
×6×4+![]() ×2
×2![]() ×2
×2![]() =36+4
=36+4![]() +2
+2![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A、B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为( )

A.y2=9xB.y2=6x
C.y2=3xD.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是底面边长为1且侧棱长为![]() 的正六棱锥
的正六棱锥![]() .
.

(1)写出直线PA与直线CD,直线PA与面ABCDEF之间的关系;
(2)求棱锥的高与斜高;
(3)求棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示是一个正三棱台,而且下底面边长为2,上底面边长和侧棱长都为1.O与![]() 分别是下底面与上底面的中心.
分别是下底面与上底面的中心.

(1)求棱台的斜高;
(2)求棱台的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.

(1)证明:MN∥平面C1DE;
(2)求点C到平面C1DE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三有![]() 名学生,按性别分层抽样从高三学生中抽取
名学生,按性别分层抽样从高三学生中抽取![]() 名男生,
名男生,![]() 名女生期未某学科的考试成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图.
名女生期未某学科的考试成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图.


(1)试计算男生考试成绩的平均分![]() 与女生考试成绩的中位数(每组数据取区间的中点值);
与女生考试成绩的中位数(每组数据取区间的中点值);
(2)根据频率分布直方图可以认为,男生这次考试的成绩服从正态分布![]() ,试计算男生成绩落在区间
,试计算男生成绩落在区间![]() 内的概率及全校考试成绩在
内的概率及全校考试成绩在![]() 内的男生的人数(结果保留整数);
内的男生的人数(结果保留整数);
(3)若从抽取的![]() 名学生中考试成绩优势(
名学生中考试成绩优势(![]() 分以上包括
分以上包括![]() 分)的学生中再选取
分)的学生中再选取![]() 名学生,作学习经验交流,记抽取的男生人数为
名学生,作学习经验交流,记抽取的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据,若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,AB=AP=3,AD=PB=2,E为线段AB上一点,且AE︰EB=7︰2,点F、G分别为线段PA、PD的中点.

(1)求证:PE⊥平面ABCD;
(2)若平面EFG将四棱锥P-ABCD分成左右两部分,求这两部分的体积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com