
【题目】几何体三视图如图所示,其中俯视图为边长为![]() 的等边三角形,则此几何体的体积为__________.
的等边三角形,则此几何体的体积为__________.

【答案】![]()
【解析】根据几何体的三视图可以判断直观图为

它是从棱柱正三棱柱上切掉几何体![]() 后剩余的几何体.可以将该几何体分为棱锥
后剩余的几何体.可以将该几何体分为棱锥![]() 和棱锥
和棱锥![]() .其中,
.其中, ![]() .点
.点![]() 到面
到面![]() 的距离为正三角形
的距离为正三角形![]() 的高,所以
的高,所以![]() .两者加起来得到
.两者加起来得到![]() .
.
故本题正确答案为![]() .
.
点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系,遵循“长对正,高平齐,宽相等”的基本原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.由三视图画出直观图的步骤和思考方法:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
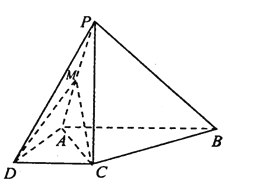
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题.该企业为了检查生产该产品的甲,乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表1是甲流水线样本的频数分布表,图1是乙流水线样本的频率分布直方图.

(1)根据图,1估计乙流水线生产产品该质量指标值的中位数;
(2)若将频率视为概率,某个月内甲,乙两条流水线均生产了5000件产品,则甲,乙两条流水线分别生产出不合格品约多少件?
(3)根据已知条件完成下面![]() 列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?
列联表,并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲,乙两条流水线的选择有关”?

附: ![]() (其中
(其中 为样本容量)
为样本容量)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的乒乓球被指定为乒乓球比赛专用球.日前有关部门对某批产品进行了抽样检测,检测结果如下表所示:
抽取球数n | 50 | 100 | 200 | 500 | 1 000 | 2 000 |
优等品数m | 45 | 92 | 194 | 470 | 954 | 1 902 |
优等品频率 |
(1)计算表中乒乓球为优等品的频率.
(2)从这批乒乓球产品中任取一个,检测出为优等品的概率是多少?(结果保留到小数点后三位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系.已知曲线
轴的正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() .倾斜角为
.倾斜角为![]() ,且经过定点
,且经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(Ⅰ)写出直线![]() 的参数方程的标准形式,并求曲线
的参数方程的标准形式,并求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出圆![]() 的直角坐标方程;
的直角坐标方程;
(2)已知圆![]() 与
与![]() 轴相交于
轴相交于![]() ,
, ![]() 两点,直线
两点,直线![]() :
: ![]() 关于点
关于点![]() 对称的直线为
对称的直线为![]() .若直线
.若直线![]() 上存在点
上存在点![]() 使得
使得![]() ,求实数
,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面内,以坐标原点O为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() (
(![]() ),圆
),圆![]() (
(![]() ),若圆
),若圆![]() 的一条切线
的一条切线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(1)当![]() ,
, ![]() 时,若点
时,若点![]() 都在坐标轴的正半轴上,求椭圆
都在坐标轴的正半轴上,求椭圆![]() 的方程;
的方程;
(2)若以![]() 为直径的圆经过坐标原点
为直径的圆经过坐标原点![]() ,探究
,探究![]() 是否满足
是否满足![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com