Question

【题目】如图，在四棱锥中，底面ABCD是菱 形，PA＝PB，且侧面PAB⊥平面ABCD，点E是AB的中点.

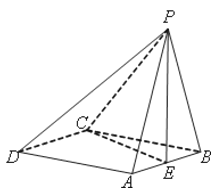
(1)求证：PE⊥AD；

(2)若CA＝CB，求证：平面PEC⊥平面PAB．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】试题分析：(1)因为PA=PB，点E是棱AB的中点，可知PE⊥AB，因为平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB，PE平面PAB，推断出PE⊥平面ABCD，进而根据线面垂直的性质可知PE⊥AD．
（2）因为CA=CB，点E是棱AB的中点，进而可知CE⊥AB，（Ⅱ）可得PE⊥AB，进而判断出AB⊥平面PEC，根据面面垂直的判定定理推断出平面PAB⊥平面PEC．

试题解析：

（1）因为PA＝PB，点E是棱AB的中点，所以PE⊥AB，

因为平面PAB⊥平面ABCD，平面PAB∩平面ABCD=AB， 平面PAB，所以PE⊥平面ABCD，

因为平面ABCD，所以PE⊥AD.

（2）因为CA＝CB，点E是AB的中点，所以CE⊥AB.

由（1）可得PE⊥AB，又因为，所以AB⊥平面PEC，

又因为平面PAB，所以平面PAB⊥平面PEC.