
【题目】
(1)已知点M(1,-3),N(1,2),P(5,y),且∠NMP=90°,则log8(7+y)=.
(2)若把本题中“∠NMP=90°”改为“log8(7+y)= ![]() ”,其他条件不变,则∠NMP=.
”,其他条件不变,则∠NMP=.
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】小明需要购买单价为3元的某种笔记本.他现有10元钱,设他购买时所花的钱数为自变量x(单位:元),笔记本的个数为y(单位:个),若y可以表示为x的函数,则这个函数的定义域为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是 ![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a、b、c分别是△ABC的三个内角A、B、C的对边.
(1)若△ABC面积S△ABC= ![]() ,c=2,A=60°,求a、b的值;
,c=2,A=60°,求a、b的值;
(2)若a=ccosB,且b=csinA,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,正确的是( )
A.斜率相等的两条直线一定平行
B.若两条不重合的直线l1 , l2平行,则它们的斜率一定相等
C.直线l1:x=1与直线l2:x=2不平行
D.直线l1:( ![]() -1)x+y=2与直线l2:x+(
-1)x+y=2与直线l2:x+( ![]() +1)y=3平行
+1)y=3平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥 ![]() 中,
中, ![]() 平面
平面 ![]() ,
, ![]() ∥
∥ ![]() ,
, ![]() ,
,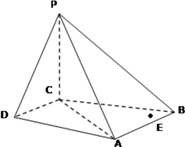
(1)求证: ![]() 平面
平面 ![]()
(2)求证:平面 ![]() 平面
平面 ![]()
(3)设点 ![]() 为
为 ![]() 中点,在棱
中点,在棱 ![]() 上是否存在点
上是否存在点 ![]() ,使得
,使得 ![]() ∥平面
∥平面 ![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com