
【题目】设函数f(x)=ex+x﹣2,g(x)=lnx+x2﹣3,若实数a,b满足f(a)=0,g(b)=0,则( )
A.0<g(a)<f(b)
B.f(b)<g(a)<0
C.f(b)<0<g(a)
D.g(a)<0<f(b)
【答案】D
【解析】解:∵y=ex和y=x﹣2是关于x的单调递增函数,
∴函数f(x)=ex+x﹣2在R上单调递增,
分别作出y=ex , y=2﹣x的图象如右图所示,
∴f(0)=1+0﹣2<0,f(1)=e﹣1>0,
又∵f(a)=0,
∴0<a<1,
同理,g(x)=lnx+x2﹣3在R+上单调递增,g(1)=ln1+1﹣3=﹣2<0,g( ![]() )=
)= ![]() +(
+( ![]() )2﹣3=
)2﹣3= ![]() >0,
>0,
又∵g(b)=0,
∴1 ![]() ,
,
∴g(a)=lna+a2﹣3<g(1)=ln1+1﹣3=﹣2<0,
f(b)=eb+b﹣2>f(1)=e+1﹣2=e﹣1>0,
∴g(a)<0<f(b).
故选:D.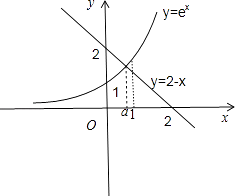
【考点精析】本题主要考查了函数单调性的性质的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数,
是奇函数,
(1)求a的值;
(2)试判断f(x)在(﹣∞,+∞)的单调性,并请你用函数单调性的定义给予证明;
(3)若对任意的t∈R,不等式f(mt2+1)+f(1﹣mt)<0恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄大点频率分布及支持“生育二胎”人数如下表:
年龄 |
|
|
|
|
|
|
频率 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:

(2)若对年龄在![]() 的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是圆心为
是圆心为![]() 的圆
的圆![]() 上的动点,点
上的动点,点![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)矩形![]() 的边所在直线与曲线
的边所在直线与曲线![]() 均相切,设矩形
均相切,设矩形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E: ![]() (a>b>0),其长轴长是短轴长的
(a>b>0),其长轴长是短轴长的 ![]() 倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2
倍,过焦点且垂直于x轴的直线被椭圆截得的弦长为2 ![]() .
.
(1)求椭圆E的方程;
(2)设过右焦点F2且与x轴不垂直的直线l交椭圆E于P,Q两点,在线段OF2(O为坐标原点)上是否存在点M(m,0),使得以MP,MQ为邻边的平行四边形是菱形?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是递增的等差数列,a1 , a2是方程x2﹣4x+3=0的两根.
(1)求数列{an}的通项公式;
(2)求数列{ ![]() }的前n项和Sn .
}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有这样一则问题:“今有良马与弩马发长安,至齐,齐去长安三千里,良马初日行一百九十三里,日增一十三里;弩马初日行九十七里,日减半里,良马先至齐,复还迎弩马.”则现有如下说法:
①弩马第九日走了九十三里路;
②良马前五日共走了一千零九十五里路;
③良马和弩马相遇时,良马走了二十一日.
则以上说法错误的个数是( )个
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com