Question

【题目】已知函数f（x）= ，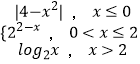

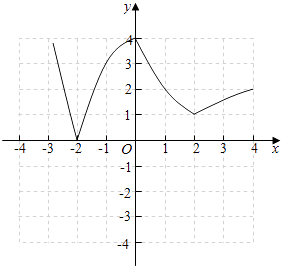
（1）画出函数f（x）的图象；
（2）求f（f（3））的值；
（3）求f（a2+1）（a∈R）的最小值．

Answer 1

【答案】
（1）解：作出函数图象如右图所示

（2）解：∵f（3）=log23，∴0＜f（3）＜2，

∴f（f（3））=f（log23）=2 = =

（3）解：由函数图象可知f（x）在[1，2]上是减函数，在（2，+∞）上是增函数，

∵a2+1≥1，

∴当a2+1=2时，f（a2+1）取得最小值f（2）=1．

【解析】（1）在每个区间段作出函数图像，（2）代入解析式，得到f（f（3））的值，（3）由图象得出f（x）的单调性，故当a2+1=2时，f（a2+1）取得最小值f（2）=1．
【考点精析】本题主要考查了函数的图象和函数的最值及其几何意义的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值；利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．